ответ: 2
![arcsin \alpha \in [-\dfrac{\pi}{2};\dfrac{\pi}{2}],arccos\alpha \in [0;\pi] \:\:\forall \alpha \in R=arcsin(y-x)+arccos(x+y)\leq \dfrac{3\pi}{2}=2\pi-arcsin(y-x)-arccos(x+y)\geq 2\pi-\dfrac{3\pi}{2}0](/tpl/images/1037/3691/e7492.png)
То есть неравенство верно для всех действительных значениях переменных, удовлетворяющих области определения. Найдем ее:
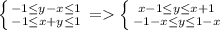
Построив 2 области и найдя их пересечение, получим область, расположенную на прикрепленном изображении на пересечении черной и красной областей (1ое и 2ое соот-но неравенства системы).
Как видим получился квадрат (1. все углы равны 90, т.к. границы задают две пары параллельных прямых, причем коэффициенты при x в парах уравнений этих прямых равны 1 и -1; 2. Все стороны равны в силу симметрии фигуры относительно осей координат) со стороной 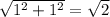
Тогда площадь равна 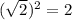
![Фигура f задаётся на координатной плоскости неравенством [tex]2\pi -arcsin(y-x)-arccos(x+y)\geq 0[/t](/tpl/images/1037/3691/eea82.jpg)
P=22 cм
Пошаговое объяснение:
Пусть К, Р, M, N - середины сторон соответственно АВ, BC, CD, AD, тогда
В ΔABD: AK = KB, AN = ND ⇒ KN - средняя линия
" Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны "
KN || BD, KN = BD/2
В ΔBCD: BP = PC, CM = MD ⇒ PM - средняя линия
PM || BD, PM = BD/2
Значит, KN || PM , KN = PM
Из этого следует, что четырёхугольник KPMN - параллелограмм (по признаку параллелограмма)
KN = BD/2 , KP = AC/2
Р kpmn = 2•(KN + KP) = 2•(BD/2 + AC/2) = BD + AC = 12 + 10 = 22 см