1 км, 20 км
Пошаговое объяснение:
Заметим, что в период с 8 до 10 часов (10 - 8 = 2 часа) расстояние до горы уменьшилось лишь на 8 - 6 = 2 км, то есть туристы сначала двигались по направлению к горе, а затем медленно стали от неё удаляться, а за период с 10 до 11 часов (11 - 10 = 1 час) оно резко увеличилось на 13 - 6 = 7 км, значит туристы уже оставили гору позади и начали стремительно удаляться от неё.
Учитывая, что они двигались с постоянной скоростью всё время, и за 3 часа (с 8 до 11 часов) изменилось на 8 + 13 = 21 км, можно сделать вывод, что они шли со скоростью 21 / 3 = 7 км/ч. Поскольку за час они проходили 7 км, и расстояние до горы с 10 до 11 часов также увеличилось на 7 км, делаем вывод, что гора находилась на прямой, по которой двигались туристы. Тогда в 9 часов расстояние до неё составляло 8 - 7 = 1 км, а в 12 часов оно составит 13 + 7 = 20 км.
P.S. Доказать, что гора находится на прямой, по которой идут туристы, можно, построив наклонные из точки, не лежащей на прямой (горы), к точкам, лежащим на прямой (местоположениям группы) и находящимся на одинаковом расстоянии друг от друга (например, равном X). Тогда расстояния до горы в 8 и 10 часов и пройденный туристами за это время путь образуют треугольник со сторонами 8, 6 и 2X км. Из неравенства треугольника (длина двух сторон треугольника больше длины его третьей стороны) следует неравенство:
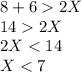
Однако, если построить соответствующий треугольник для расстояний до горы в 10 и 11 часов, то получим следующее неравенство:
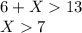
Эти неравенства противоречат друг другу, следовательно данная точка (гора) не может не лежать на прямой, по которой идут туристы, и расстояние, проходимое ими за час, равно 7 км/ч.
20 машин.
Пошаговое объяснение:
Пусть первоначальная грузоподъёмность машины была х т, тогда 60/х машин должны были использовать по плану.
В действительности на каждую машину грузили (х-0,5) т, поэтому машин потребовалось 60/(х-0,5) штук.
Зная, что дополнительно задействовано 4 машины меньшей грузоподъёмности, составим и решим уравнение:
60/(х-0,5) - 60/х = 4
Домножим обе части уравнения на х(х-0,5) ≠ 0, получим
60х - 60(х-0,5) = 4х(х-0,5)
60х - 60х + 30 = 4х² - 2х
30 = 4х² - 2х
4х² - 2х - 30 = 0
2х² - х - 15 = 0
D = 1 + 120 = 121
x1 = (1+11)/4 = 3;
x2 < 0, не подходит по смыслу задачи.
3 т планировалось грузить на машину первоначально,
60/3 = 20 (машин) планировалось использовать