Правило сложения: Пусть объект А мы можем выбрать из множества , а объект В можно выбрать , то объект «А+В» можно выбрать .
Возможно, это правило покажется непосвященному человеку абракадаброй, но ничего сложного нет. Рассмотрим пример – пусть в одном ящике есть m шариков, а во втором ящике – n шариков. Сколькими можно вытащить шарик из одного этих ящиков. Очевидно, что ОДИН шарик можно достать .
Правило умножения: Пусть объект А выбирается , объект В выбирается , то оба объекта можно выбрать .
Все очень просто – каждый из выбора объекта А комбинируется с каждым из выбора объекта В, то есть количество просто умножается друг на друга
Пошаговое объяснение:
|x|+|y| = 2
если решать "в лоб", то надо было бы раскрывать модули,
но рассмотрим специфику уравнения.
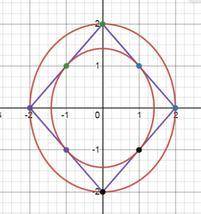
тут видно, что график данного уравнения симметричен относительно обеих осей (это такой квадрат "на боку"). (т.е. все четыре возможных графика (которые получатся при раскрытии модулей) при пересечении образуют квадрат со стороной 2√2)
теперь второе уравнение
это окружность. чтобы квадрат и окружность соприкасались только в 4 точках, окружность должна быть
1) вписана в квадрат, т.е радиус ее должен быть равен половине стороны квадрата, те. 2√2 /2 = √2
и тогда параметр а = (√2)² = 2
х² + у² = 2
2) описана вокруг квадрата, т.е. ее радиус должен быть = половине диагонали квадрата =2
и тогда а = (2)² = 4
x² + y² = 4
сумма всех решений 2+4=6
Их разность равна 90