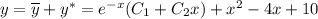14.4 см
Пошаговое объяснение:
Побудуємо прямокутник ABCD, та проведемо в ньому діагоналі АС і BD, а також висоту DO до діагоналі АС і висоту EK із точки перетину діагоналей до більшої сторони AD.
Приймемо, що ОС=х,
тоді АС=4х.
Так як діагоналі прямокутника рівні і точкою перетину діляться навпіл, то АЕ=СЕ=ЕD=2х
і OE=CE-OC ⇒ OE=2x-x ⇒ OE=x.
Так як точка перетину діагоналей прямокутника є його геометричним центром, то CD=2EK=7.2 см.
Тоді, із прямокутного ΔCDO маємо:
OD²=CD²-OC² ⇒ OD²=51.84 - x²
Із прямокутного ΔEDO маємо:
OD²=ED²-OE² ⇒ OD²=4x² - x² ⇒ OD²=3x²
Отримуємо вираз:
51.84 - x² = 3x²
4x²=51.84
x=3.6
Тоді довжина діагоналі:
АС=4х=14.4 см
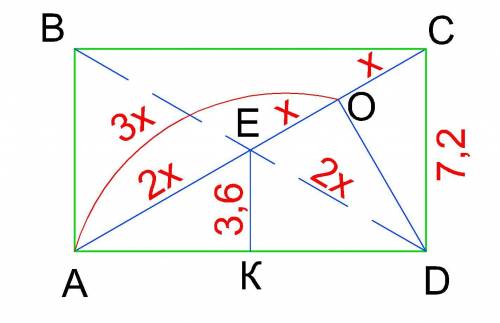
Найдем начала общее решение соответствующего однородного дифференциального уравнения
(*)
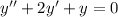Воспользовавшись заменой Эйлера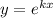 
, мы получим характеристическое уравнение
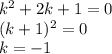
Общее решение уравнения (*)
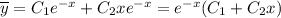
Далее нужно найти частное решение. Рассмотрим функцию:
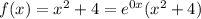
Здесь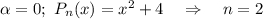 
Сравнивая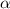 
с корнями характеристического уравнения и, принимая во внимая, что 
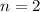частное решение будем искать в виде
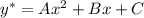
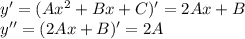
Подставляем все это в исходное дифференциальное уравнение
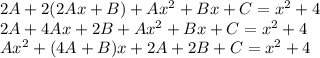
Приравниваем коэффициенты при степени x
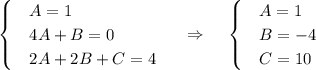
Частное решение: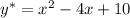 
Общее решение линейного неоднородного дифференциального уравнения:
