1. Путь меньшее из двух чисел х, тогда большее число (10х+у), где у - последняя цифра числа. 10х+у+х=2011 11х+у=2011 Необходимо найти такое число х, при котором 11х будет наибольшим, но при этом меньше 2011. 11х<2011 x<2011/11 x<182 9/11 Значит х=182 первое число 2011-182=1829 второе число ответ 182 и 1829 искомые числа
2. Пусть искомое число abc. По условию задачи: а+b+c=9 c=9-a-b
(100a+10b+c)=(100c+10b+a)*36/47 47(100a+10b+c)=(100c+10b+a)*36 4700a+470b+47c=3600c+360b+36a 4664a+110b=3553c 424a+10b=323c 424a+10b=323(9-a-b) 424a+10b=2907-323a-323b 747a+333b=2907 83a+37b=323 a+37/83b=323/83 Поскольку а и b целые, то дальше только методом подбора: a=3 b=(323-83*3)/37=2 c=9-2-3=4 Значит искомое трехзначное число: 324
Задача немного не логичная, ну да ладно.
Запишем условие:
Число страниц во второй книге равно 60% от числа страниц в первой книге.
Число страниц в третьей книге равно 2/3 страниц в первой книге.
Всего страниц в 3-ех книгах: 136*3=408 страниц.
За икс целесообразно принят кол-во страниц в первой книге:x.
Тогда во второй книге получаем: 0,6*x;
В третьей: (2/3)*x.
Составляем уравнение:
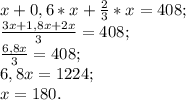
Получили, что в первой книге 180 страниц.
Тогда, во второй: 0,6*180=108 страниц.
В третьей же: 180*2/3=120 страниц.
ответ: первая книга-180 стр, вторая книга-108 стр, третья книга-120 стр.