Логарифмический ноль. Элементарное свойство, которое нужно обязательно помнить. Какое бы ни было основание логарифма, если в аргументе стоит 1, то логарифм всегда равен 0.
Логарифмическая единица. Еще одно простое свойство: если аргумент и основание логарифма одинаковы, то значение логарифма будет равно единице.
Основное логарифмическое тождество. Отличное свойство, превращающее четырехэтажное выражение в простейшую b. Суть этой формулы: основание a, возведенное в степень логарифма с основанием а, будет равно b.
Сумма логарифмов. При умножении логарифмируемых чисел, можно сделать из них сумму 2х логарифмов, у которых будут одинаковые основания. И так невычислимые логарифмы становятся простыми.
Логарифм частного. Здесь ситуация схожая с суммой логарифмов. При делении чисел мы получаем разность двух логарифмов с одинаковым основанием.
Вынесение показателя степени из логарифма. Тут действуют целых 3 правила. Все просто: если степень находится в основании или аргументе логарифма, то ее можно вынести за пределы логарифма, в соответствии с этими формулами
Формулы перехода к новому основанию. Они нужны для выражений с логарифмами, у которых разные основания. Такие формулы в основном используются при решении логарифмических неравенств и уравнений.
Пошаговое объяснение:
ответ: 26 мальчиков.
Из условия мы знаем, что в лыжных гонках участвовало 35% девочек и 100% - 35% = 65% мальчиков, то есть мальчиков было несколько больше, а точнее - на 65% - 35% = 30%, но из задачи мы также знаем, что эти 30% составляют 12 человек.
Проблема только в том,что 30 на 12 не делится! Ничего страшного! Примем только в расчет,что на каждый процент приходится на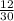 
= 
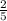человека.
Теперь домножим полученный результат на проценты и мальчиков, и девочек, и узнаем, сколько их было в лыжной гонке:
(девочек).
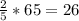(мальчиков).
И вот мы получили, что в лыжных гонках участвовало 14 девочек и 26 мальчиков.
▪1) 2 целых 2/5 ÷ 8/15=12/5÷8/15=12/5×15/8=3×3/2=9/2=4 целых 1/2=4,5
▪2) 7-4,5=2,5
▪3) 2,5 ÷ 5 целых 5/8 = 25/10 ÷ 45/8 =25/10 × 8/45 = 5/5 × 4/9 = 4/9