n! = 1*2**n
n ∈ N
a>b
Aₐᵇ = a! / (a - b)!
Cₐᵇ = a! / (a - b)!b!
Aₓⁿ⁻³ : Aₓⁿ⁻² = x!/(x - n + 3)! : x!/(x - n + 2)! = x!/(x - n + 3)! * (x - n + 2)!/x! = 1 / (x - n + 3)
(x - n + 3)! = 1*2**(x - n + 2)(x - n + 3)
(x - n + 2)! = 1*2**(x - n + 2)
(x - n + 2)! / (x - n + 3)! = (x - n + 3)
Cₓⁿ⁻³ : Cₓⁿ⁻² = x!/(x - n + 3)!(n - 3)! : x!/(x - n + 2)!(n - 2)! = x!/(x - n + 3)!(n - 3)! * (n -2)!(x - n + 2)!/x! = (n - 2) / (x - n + 3)
(n - 2)! = 1*2**(n - 4)(n - 3)(n - 2)
(n - 3)! = 1*2**(n - 4)(n - 3)
(n - 2)! / (n - 3)! = n - 2
1/( x - n + 3) = 1/8
(n - 2)/(x - n + 3) = 5/8
(n - 2) / 8 = 5/8
n - 2 = 5
n = 7
x - n + 3 = x - 7 + 3 = x - 4 = 8
x = 12
(см. объяснение)
Пошаговое объяснение:
Приведу несколько идей к решению:
1:
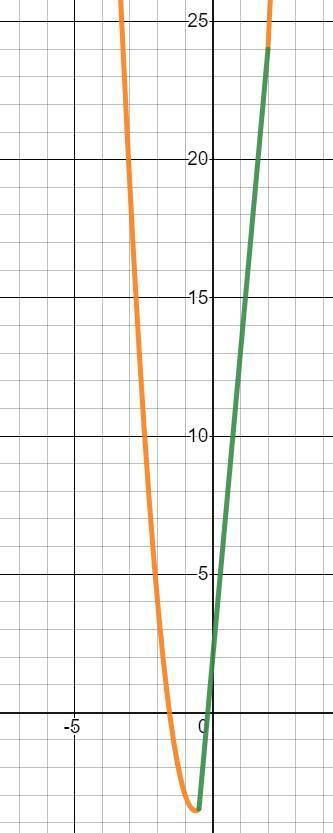
Когда видишь только буквы a (параметр) и x (переменная), то выгодно использовать достаточно универсальный прием: методику построения в координатах (x; a) /или/ (a; x). Тогда у тебя получатся парабола и прямая, склеивающиеся в общих точках (см. прикрепленный файл; построение в координатах (x; a); прямая выделена зеленым; парабола оранжевым). Теперь просто двигаешь горизонтальную прямую вверх и вниз и смотришь пересечения. Единственное решение достигается при 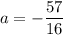 ; решений нет при
; решений нет при 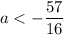 .
.
2:
Другим хорошим может стать построение левой и правой частей уравнения по-отдельности. Для левой части строим параболу 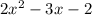 и симметрично отражаем все, что под осью x. Для правой части будет парабола, которая бегает вверх или вниз в зависимости от значения параметра. Единственное решение возможно, только когда
и симметрично отражаем все, что под осью x. Для правой части будет парабола, которая бегает вверх или вниз в зависимости от значения параметра. Единственное решение возможно, только когда 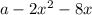 касается
касается 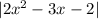 , откуда
, откуда 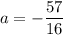 . Здесь стоит остановиться на том, как считать a:
. Здесь стоит остановиться на том, как считать a: 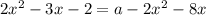 (обратите внимание, что здесь можно не писать модуль)
(обратите внимание, что здесь можно не писать модуль)  . Берем дискриминант и приравниваем к нулю:
. Берем дискриминант и приравниваем к нулю: 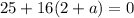 . Откуда получаем требуемое значение. Если
. Откуда получаем требуемое значение. Если 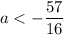 , то решений нет.
, то решений нет.
3:
Пусть 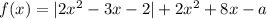 . Тогда:
. Тогда: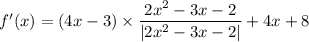 . Решив
. Решив 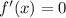 , получаем, что
, получаем, что  . Просчитав знаки, делаем вывод, что функция убывает до
. Просчитав знаки, делаем вывод, что функция убывает до  , а затем возрастает при любом значении параметра. Тогда достаточно решить
, а затем возрастает при любом значении параметра. Тогда достаточно решить 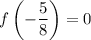 , откуда
, откуда 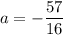 . Таким пользоваться не рекомендую.
. Таким пользоваться не рекомендую.
Задание выполнено!
Жизнь человека становится зависимой не от привычных критериев — образования, профессиональных, навыков, материального положения и т.д., а совсем от других—солнечной радиации, силы ветра, температуры воздуха, от наличия или отсутствия водоемов, животных, съедобных растений.
Благоприятный исход автономного существования во многом зависит от психофизических качеств человека, физической подготовленности, выносливости. Но этого нередко оказывается недостаточно для Главный постулат выживания — человек может и должен сохранить здоровье и жизнь в самых суровых физико-географических условиях если он сумеет использовать в своих интересах все, что дает окружающая среда.