Пошаговое объяснение:
12.3) Домножим на 2 первое уравнение и сложим со вторым:
7z = 14i + 7 => z = 2i + 1;
12.4) произведение комплексного числа на его сопряжённое равно модулю этого комплексного числа. Представим z в виде x + yi. Значит первое уравнение системы преобразуется в:
4 <= x^2 + y^2 <=49. если выражение в середине равно 4, то мы получаем уравнение окружности с радиусом 2. Если равно 49 - то с радиусом 7. Мы получаем множество точек, ограниченных двумя окружностями. Так как вещественная часть числа z равна x, то второе условие можно записать, как:
-2 <= x <= 5. Это обрезает окружность вертикальными прямыми, проходящими через точки на оси Re -2, 5. Все границы получившейся фигуры включены. Сам график мне рисовать лень.
12.5) а) Так как у числа отсутствует вещественная часть, число лежит на мнимой прямой и фаза числа равна π/2 + 2πk, k - целое число. cos φ = 0, sin φ = 1. Откуда:
-3i = -3 * (cos(π/2 + 2πk) + i * sin(π/2 + 2πk));
б) Как я понимаю нужно преобразовать. cos π/6 = sqrt(3)/2, sin π/6 = 1/2. Откуда следует, что z = -sqrt(3)/2 + 0,5i
12.6) Представим число z^4 в тригонометрической форме:
-1 = Acos φ; sqrt(3) = Asin φ.
Проделим второе уравнение на первое:
tan φ = -sqrt(3). tan π/3= sqrt(3). Значит tan (-π/3) = -sqrt(3), откуда:
φ = -π/3 + 2πk.
Значит cos φ = -1/2, sin φ = sqrt(3)/2. Подставляя в первые уравнения получаем A = 2. Там же можно и проверить фазу. Получаем представление числа в тригонометрической форме:
z^4 = 2 * (cos(-π/3 + 2πk) + i*sin(-π/3 + 2πk));
Откуда по формуле Муавра очень легко можно вычислить корень 4-ой степени. Далее sqrt4(2) - корень 4-ой степени из 2.
z = sqrt4(2) * (cos F + i*sin F), где F = (-π/3 + 2πN)/4, где в свою очередь N - номер одного из 4-х корней (от 0 до 3-х).
12.7) а) D = 16 - 4 * 5 = -4 = (2i)^2;
z1,2 = ((+-)2i + 4)/2 = (+-)i + 2;
б) D = -81 + 4 * 14 = -25 = (5i)^2;
z1,2 = ((+-)5i + 9i)/2 = ((+-)2,5 + 4,5)i
Фух, вроде всё
7.
Из обратно теоремы о пропорциональных отрезков, если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные или пропорциональные между собой отрезки, начиная от вершины, то такие прямые параллельны. Отсюда следует, что:
Отрезки MN и NK параллельны отрезкам BC и AD, а значит, и весь отрезок MK || основам трапеции (BC || AD). MK — средняя линия трапеции, т.к. точка М делит сторону AB пополам.
Формула для нахождения ср. линии трапеции:
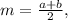
где a и b — основы трапеции.
Подставляем значения:
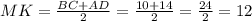
ответ: MK = 12.
8. EM || BC || AD по теореме о пропорциональных отрезках. EM — средняя линия трапеции. Все отрезки, образующие среднюю линию EM параллельны основам трапеции.
Найдем EM:
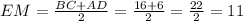
Средняя линия делит диагонали пополам.
Р-м ΔABC и ΔDCC: EK и LM — средние линии.
Средняя линия треугольника равна половине стороны к которой она параллельна. Находим длины этих отрезков.
EK = LM = DB/2 = 6/2 = 3.
Находим KL: EM − (EK+LM) = 11−(3+3) = 5
ответ. KL = 5.
9. ABCD — равнобедренная трапеция. MF — средняя линия, AM = MB = CF = FD = 2. BC = EK = 2. BE и CK — высоты трапеции.
Р-м прямоугольные треугольники ABE и DKC: ∠A = ∠D = 60°. Значит ∠AEB и ∠KCD — по 30°.
Катет, лежажий напротив угла, синус которого 30°, равен половине гипотенузе. AE/KD = AB/CD/2= 2.
AD = 2*2+2 = 6
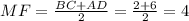
ответ: MF = 4.
2) 100-95=5(%)- 104 дерева
3) 35:5=7- разница между 1 и 2 группой
4) 104*7= 728(д.)- 2 группа
5) 104+728=832(д.) - 2 и 3 группы
6) 60:5=12- разница между 1 и 3 группой
7) 104*12=1248(д.)- 1 группа
8) 1248+832=2080(д.)
ответ: всего 2080 деревьев