Відповідь:
1) область определения функции y=x ln x от нуля до бесконечности, не включая нуль
2) y(-x)=-x ln x - общего вида.
3) точки пересечения с осями:
Oy, но х≠ 0, значит точек пересечения с осью y нет.
Ox: y=0, то есть x ln x=0
x=0 или ln x=0
0 ¢ D(y) x=e0
x=1
(1;0) – точка пересечения с осью х
4) Найдем производную функции:
y’=x’ ln x + x(ln x)’=ln x +1
5) критические точки:
y’=0, то есть ln x +1=0
ln x=-1
x=e-1
x=1/e (≈ 0,4)
y’=0 , если x=1/e , значит x=1/e – критическая точка.
6) Обозначим критические точки на координатной прямой и определим знак
функции:
-1/e
- +
1/e
x=1/(2e); y’=log(2e)-1+1=1-ln(2e)=1-ln e=-ln 2<0
x=2e; y’=ln(2e)+1=ln 2+ln e+1=ln 2+2>0
7) Так как на промежутке (0;1/е) y'(x)<0 то на этом промежутке функция убывает
Так как на промежутке (1/е; бесконечность) y'(x)>0 то на этом промежутке функция возрастат.
Следовательно точка х=1/е является точкой минимума.
8) экстремумы функции:
ymin=y(1/e)=1/e ln e-1=-1/e (≈ -0,4).
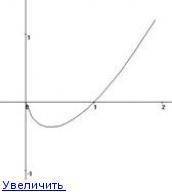
9)
Горизонтальной асимптоты у функции нет, поскольку предел функции при стремлении х в плюс бесконечность равен плюс бесконечности.
Вертикальные асимптомы- подозреваемая точка х=0(граница области определения).Чтобы узнать, будет ли х=0 вертикальной асимптотой надо найти предел функции при х стремящемся к нулю справа. этот предел равен нулю. Следовательно, по определению, х=0 не является вертикальной асимптотой.
Наклонные асимптоты. Если они и есть, то только правые (слева область определения ограниченна 0).
по теореме о существовании наклонных асимптот, если существуют конечные lim f(x)/x =k и lim f(x)-kx =b (х в обоих случаях стремится к плюс бесконечности, раз ищем правую асимптоту) , то y=kx+b будет наклонной асимптотой.
вычисляя lim f(x)/x получаем бесконечность, следовательно, наклонных асимптот нет.
Таким образом, у функции нет асимптот.
Покрокове пояснення:
E) 3; 1; -1; -3.
E) I, III .
Пошаговое объяснение:
1) 3 - 2•(n-1)
Если n = 1, то 3 - 2•(1 - 1) = 3;
Если n = 2, то 3 - 2•(2 - 1) = 1;
Если n = 3, то 3 - 2•(3 - 1) = - 1;
Если n = 4, то 3 - 2•(4 - 1) = - 3;
и так далее.
Получим
E) 3; 1; -1; -3.
2) Рассмотрим последовательность
I. -1; -1; 1; 3; 7.
Проверим выполнение условия:
"начиная со второго члена, каждый последующий будет суммой двух предыдущих членов и 3".
1 = - 1 + (- 1) + 3; 1 = 1 - верно.
3 = 1 + (- 1) + 3; 3 = 3 - верно.
7 = 1 + 3 + 3; 7 = 7 - верно.
Рассмотрим последовательность
II. -2; 1; 2; 3; 8.
Проверим выполнение условия:
2 = - 2 + 1 + 3; 2 = 2 - верно.
3 = 2 + 1 + 3; 3 = 6 - неверно.
Рассмотрим последовательность
III. 1,4; 2,1; 6,5; 11,6; 21,1
Проверим выполнение условия:
6,5 = 1,4 + 2,1 + 3; 6,5 = 6,5 - верно;
11,6 = 6,5 + 2,1 + 3; 11,6 = 11,6 - верно;
21,1 = 11,6 + 6,5 + 3; 21,1 = 21,1 - верно.
Получим
E) I, III .
1.40 мм=4 см
ширина =8-4=4 см
площадь=8*4=32 кв см