В прямоугольном параллелепипеде все грани - прямоугольники, все рёбра равны и перпендикулярны основаниям.
Формула диагонали квадрата d=a√2 ⇒
Диагональ АС основания равна 4√2
Из прямоугольного треугольника АА1С по т.Пифагора боковое ребро
АА1=√(А1С²-AC²)=√(81-32)=7 (ед. длины)
-------
Вариант решения.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Измерениями прямоугольного параллелепипеда являются длины трех ребер, исходящих из одной его вершины. Отсюда следует:
D²=a²+b²+c², где а и b- стороны основания, с - боковое ребро.
По условию а=b=4. D=9
81=16+16+c² ⇒
c²=81-32=49
c=7 - длина бокового ребра.

Чтобы найти сколькими нулями оканчивается произведение нужно найти сколько раз в этом произведении встречается множитель 10.
Заметим, что 10 раскладывается на простые множители как 10=2·5. Очевидно, сомножителей "2" будет больше чем сомножителей "5". Таким образом, нужно узнать число множителей "5" в произведении. Каждый такой множитель в паре с множителем "2" даст множитель "10" и соответственно дополнительный ноль на конце числа.
Найдем, сколько чисел содержит множитель "5". Всего среди первых 2020 натуральных чисел таких чисел 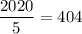 , но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
, но в данном произведении отсутствуют первых три числа кратные 5 (5, 10, 15). Значит, множитель "5" содержит 404-3=401 число.
Но некоторые числа содержат не один множитель "5", а два. Найдем количество таких чисел.
Для этого разделим 2020 на 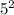 :
:
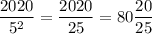
Значит, последнее число, которое содержит в своем составе два множителя "5" - это число  . Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
. Первое такое число - очевидно, 25. Значит, всего таких чисел 80.
Еще некоторые числа содержат три множителя "5". Найдем количество таких чисел. Для этого разделим 2020 на 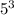 :
:
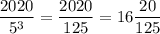
Значит, последнее число, которое содержит в своем составе три множителя "5" - это число 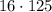 . Первое такое число - 125. Значит, всего таких чисел 16.
. Первое такое число - 125. Значит, всего таких чисел 16.
И, наконец, некоторые числа содержат сразу четыре множителя "5". Найдем их количество. Для этого разделим 2020 на 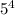 :
:
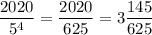
Значит, последнее число, которое содержит в своем составе четыре множителя "5" - это число 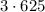 . Первое такое число - 625. Значит, всего таких чисел 3.
. Первое такое число - 625. Значит, всего таких чисел 3.
Чисел, кратных 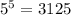 среди множителей нет.
среди множителей нет.
Итак, 401 число содержат в своем составе множитель "5", 80 чисел содержат второй множитель "5", 16 чисел содержит третий множитель "5" и 3 числа содержат четвертый множитель "5". Значит, всего множителей "5" имеется:
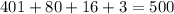
Значит, число 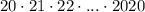 оканчивается 500 нулями.
оканчивается 500 нулями.
ответ: 500
S = A • C • D