Правильная четырехугольная пирамида 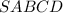 .
.
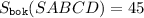 (см²).
(см²).
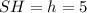 (см).
(см).
 - сторону основания.
- сторону основания.
Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
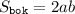 , где
, где  - сторона основания и
- сторона основания и 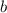 - апофема (высота боковой грани, проведенная из вершины).
- апофема (высота боковой грани, проведенная из вершины).
Попробуем выразить 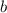 через
через  (сторону основания) и
(сторону основания) и 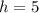 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный 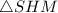 (где
(где 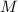 - середина
- середина 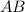 ). В нем
). В нем 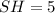 (см), а
(см), а 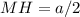 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
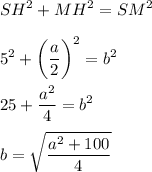
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что  - неотрицательное):
- неотрицательное):
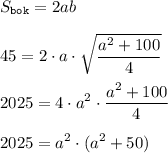
Пусть 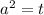 :
:
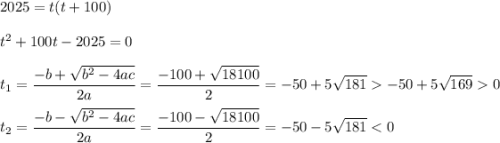
Второй корень нам не подходит по причине отрицательности. Значит:
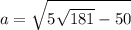
Задача решена!
ответ: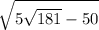 или около
или около 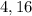 (см).
(см). 
треугольник АВС, АН=30 и СМ=39 медианы, АМ=МВ, ВН=НС, МН-средняя линия треугольника=1/2АС=26/2=13, АМНС - трапеция, МН параллельна АС, из точки Н проводим линию параллельную СМ до пересечения ее с продолжением АС в точке Е, ЕН=СМ=39, СМНЕ- параллелограмм, СЕ=МН=13, АЕ=АС+СЕ=26+13=39
треугольникАНЕ равнобедренный, АЕ=ЕН=39, проводим высоту ЕТ=медиане=биссектрисе на АН, АТ=ТН=1/2АН=30/2=15, треугольникАТЕ прямоугольный, ЕТ²=АЕ²-АТ²=1521-225=1296, ЕТ=36, площадь АНЕ=площадь трапеции АМНС=1/2*АН*ЕТ=1/2*30*36=540, что составляет 3/4 площади АВС
(площадь треугольника отсекаемого средней линией (МН)=1/4 площади АВС, можно подсчитать самим),
площадь АВС=площадьАМНС*4/3=540*4/3=720