Пошаговое объяснение:
Zad.1.
У нас есть 3 треугольника
1) ABC-прямоугольный треугольник
S (ABC) = 1 / 2a * b = 1/2 * 4 * 3 = 2 * 3 = 6
2) AED-прямоугольный: S = 1 / 28a * b = 1/2 * 4 * 3 = 2 * 3 = 6 j
3) треугольник CAD
Здесь нам нужно рассчитать отрезки AC и AD так:
* из треугольника ABC вычисляем отрезок AC по теореме Питагора
AC ² = 4 ² + 3 ² = 16 + 9 = 25
AC = √25 = 5 j
* из треугольника AED по теореме Питагора вычислить отрезок AD
AD ² = AE ² + ED ² = 4 ² + 3 ² = 16 + 9 = 25
AD = √25 = 5j
* расчеты показывают, что треугольник CAD равносторонний, его площадь можно рассчитать по формуле S = a ²√3 / 4
S = AD ²√3 / 4 = 5²√3 / 4 = 25√3 / 4 = 6,25√3 j²
(на фото красным выделены расчетные сечения AC и AD)
Zad.2.
На прилагаемой фотографии фьюгре представляет собой прямоугольник, уменьшенный трапецией AFEG.
Фигуры S = прямоугольник S - трапеция S
Прямоугольник S = a * b = 5 * 4 = 20j ^ 2.
S трапеция = 1/2 (a + b) * h = 1/2 (2 + 1) * 1 = 3/2 = 1,5 j²
S (ABCDEF) = S (GBCD)-S(AFEG) = 20–1,5 = 19,5 j²

Пошаговое объяснение:
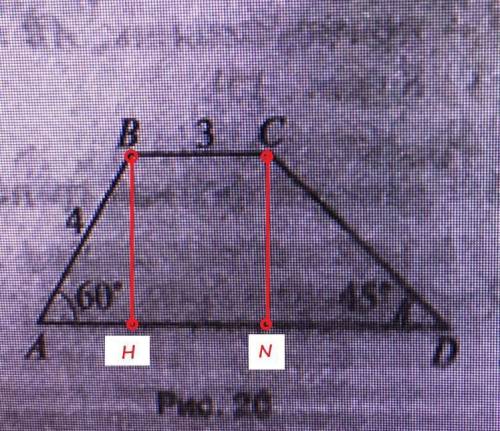
Проведем высоту ВН. Получим треугольник АВН, у которого угол АВН=30*. Тогда АН=1/2АВ=4*1/2=2.
Найдем высоту ВН.
ВН^2=FD^2-AH^2=4^2-2^2=16-4=12;
BH=√12=2√3.
Проведем высоту CN. Получим треугольник CDN, у которого угол CDN равен углу NCD и равен 45*. Следовательно треугольник CDN - равнобедренный и CN=DN. Но CN=BH=√12. Следовательно DN=CN=BH=√12=2√3.
Основание AD=AH+HN+ND=2+3+√12=5+√12.
Найдем сторону CD. CD^2=CN^2+DN^2=(√12)^2+(√12)^2=12+12=24;
CD=√24=2√6.
Периметр P(ABCD)=AB+BC+СD+AD=4+3+2√6+5+√12=2√3+2√6+12.
Площадь S(ABCD)=BH*(AD+BC)/2=2√3(5+2√3+3)/2=8√3+6.
См. скриншот.
2)16:2=8
3)80-16=67
0ответ: 8 километров дороги рабочие отремантировали за 2 дня.