Доказательство.
Пусть α и β — данные плоскости, a1 и a2 — пересекающиеся прямые в плоскости α , а b1 и b2 — соответственно параллельные им прямые в плоскости β .
Допустим, что плоскости α и β не параллельны, то есть, они пересекаются по некоторой прямой c .
Прямая a1 параллельна прямой b1 , значит, она параллельна и самой плоскости β .
Прямая a2 параллельна прямой b2 , значит, она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α , значит, хотя бы одна из прямых — a1 или a2 — пересекает прямую c , то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β , значит, пересекая прямую c , прямая a1 или a2 пересекает плоскость β , чего быть не может, так как прямые a1 и a2 параллельны плоскости β .
Из этого следует, что плоскости α и β не пересекаются, то есть, они параллельны.
Свойства параллельных плоскостей
Теорема 1. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны.
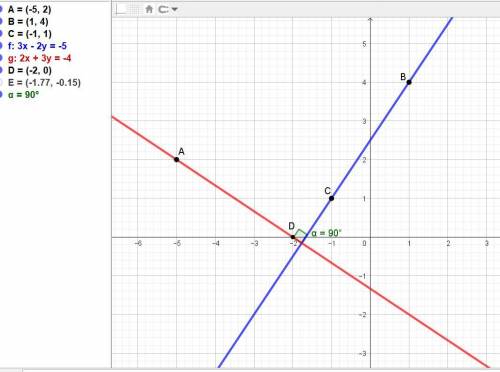
Даны три точки А(-5; 2), В(1;4), С(-1; 1). Примем точку D(x; 0).
Находим уравнение прямой BC.
Вектор BC = (-1-1; 1-4) = (-2; -3).
Получаем уравнение BC: (x - 1)/(-2) = (y - 4)/(-3)
или в общем виде: 3x - 2y + 5 = 0.
У перпендикулярной прямой в общем виде Ax + By + C = 0 коэффициенты А и В меняются на -В и А ( из условия их скалярного произведения, равного нулю).
Тогда получаем уравнение перпендикулярной прямой к ВС:
2x + 3y + C = 0.
Подставим координаты точки A(-5; 2).
2*(-5) + 3*2 + C = 0, отсюда С = 10 - 6 = 4.
Уравнение перпендикуляра 2x +3y + 4 = 0.
Для определения точки D подставим её координаты в это уравнение.
2х + 3*0 + 4 = 0, отсюда х = -4/2 = -2.
ответ: точка D(-2; 0).
5/7 - 70 км
1 - х км
х=70*1*7/5=98 км - намеченный путь