Это простейшие производные.
Рассмотрим общий случай:
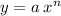
а – просто коэффициент при Х, n – степень Х.
Производная функции у, обозначаемая обычно у' или dy/dx, будет иметь следующий вид:
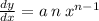
Ничего сложного.
Рассмотрим несколько частных случаев из Ваших примеров.
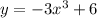
Здесь коэффициент а равен (–3), степень n равна 3. Значит, по правилу, представленному выше, производная будет иметь вид:
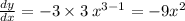
При числе 6 нет «Х», поэтому при взятии производной это число просто пропадает.
Другой частный пример:
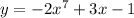
Берём производную от каждой части по отдельности.

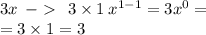

Итого:
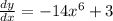
Для того чтобы ответить на этот вопрос, необходимо приравнять данную дробь к нулю, но прежде сократим это выражение:
(b^3-5b^2-4b+20) :(b^2-25)=[(b^3-5b^2)-(4b-20)] : (b^2-25)=[b^2(b-5)-4(b-5)] : (b^2-25)=(b^2-4)*(b-5) : (b-5)*(b+5)=(b^2-4)/(b+5)
(b^2-4)/(b+5)=0
(b^2-4)=0*(b+5)
b^2-4=0
b^2=4
b1,2=+-√4=+-2
b1=2
b2=-2
ответ: При b=-2 и b=2 значение дроби равно нулю