1)Пусть х см - a
(3х)см-b
S=ab
3x^2=27
x1=-3 -не удовлетворяет,так как <0
x2=3
а=3 см
b=9 см
ответ:3 см;9 см
2)Sквадрата=а^2
а^2=64 см
а=8 см
Р=а*4
Р=8*4=32 см
ответ:32 см
3)У ромба все стороны равны,а сторон 4.
Р=4*а
а=16:4
а=4 см
S=а*h(высота)
16=4*h
h=4 см
ответ:4 см
4)S=1/2 *AB(гипотенуза)*h(высота)
1/2*АВ*4=40
АВ=20 см
ответ:20 см
5)Так как трапеция прямоугл.,то большая сторона и является высотой
S=(ВС+AD)/2 *h(высота)
S=(5+13)/2*10
S=90 см^2
ответ:90 см^2
6)Сумма углов многоугольника равна 180*(n-2),где n-количество сторон
у нас сумма углов 180*3=540 градусов
Пусть х градусов приходится на одну часть
15х=36
х=36 градусов
36 градусов-первый угол
72 градусов-2 угол
108 градусов-3 угол
144 градуса-4 угол
180 градуса-5 угол
8)пусть 1 катет-х см, 2 катет-(х+2)
По теореме Пифагора находим х
х^2+x^2+4x+4=100
x^2+2x-48=0
D=49
x1=-8 - <0 не удовлетворяет
х2=6
1 катет-6 см
2 катет-8 см
Площадь прямоугольного треугольника равна половине произведения катетов.
S=6*8/2=24 кв.см.
ответ:24 кв.см.
Перепишем неравенство в таком виде
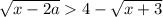 (*)
(*)
Остановимся на этом шаге. Функция справа - убывающая, очевидно наступит момент, когда она обратится в нуль и в дальнейшем будет принимать лишь отрицательные значения. Функция слева может быть лишь положительна (или равна 0), т.е. можно найти такое значение параметра, при котором
все множество значений левой функции всегда будет больше множества значений правой функции. В этом случае решением неравенства будут являться все  из области определения.
из области определения.
Найдем при каком значении переменной правая функция обращается в нуль:
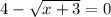
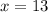
В этой точке левая функция уже должна быть определена и должна принимать значения, строго большие нуля, т.е. 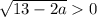 =>
=> 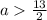 .
.
Итого при 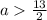 и
и 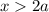 исходное неравенство выполняется.
исходное неравенство выполняется.
Следующий шаг, возведем обе части (*) в квадрат, чуть упростим, получим
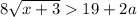 (#)
(#)
Проанализируем это неравенство. Если величина справа будет меньше нуля, то при любых допустимых  неравенство будет выполнено. Найдем момент, когда величина обращается в нуль:
неравенство будет выполнено. Найдем момент, когда величина обращается в нуль:
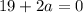 =>
=>
При значениях параметра меньших 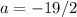 все допустимые аргументы являются решениями. Очевидно, что из двух условий
все допустимые аргументы являются решениями. Очевидно, что из двух условий 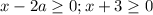 определеяющим будет
определеяющим будет
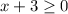
Итого при 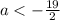 и
и 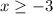 исходное неравенство выполняется.
исходное неравенство выполняется.
Последний шаг, возведем (#) в квадрат и упростим, получится выражение
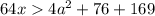
Откуда 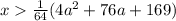 для всех оставшихся значений параметра a
для всех оставшихся значений параметра a
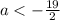 ,
, 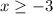
 ,
, 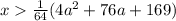
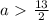 ,
, 
2×13=26(кг)-масса 13 деталей
ответ:13 деталей