Пошаговое объяснение:
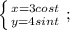
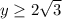
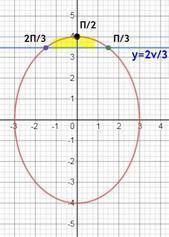
для простоты рисования графика, отмечу, что мы фактически имеем эллипс
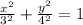
вот рисуем этот эллипс и прямую у = 2√3. в осях ох оу мы нарисовали график и видим все границы по х и у
теперь нам надо перейти к пределам интегрирования по t
у = 2√3 = 4sin t ⇒ t₁ = π/3; t₂= 2π/3
однако, мы видим, что нужная нам фигура состоит из двух симметричных относительно оси оу фигур. найдем площадь одной и умножим потом на 2
надл найти "высшую" точку эллипса. это будет точка при х = 0
х = 0 = 3cost ⇒ t = π/2
вот и все, теперь считаем интергал
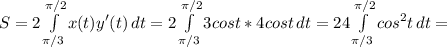
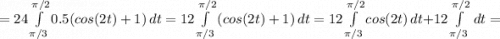
теперь для первого интеграла мы сделаем замену u=2t; du=2dt, тогда в этом интеграле поменяются пределы интегрирования
верхний станет π, а нижний 2π/3, и вот
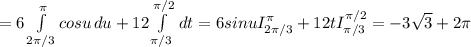
Y = x² - 2x - 3.
Точка перегиба - нуль второй производной.
Первая производная
Y' = 2x - 2
Вторая производная
Y" = 2 = const
Эта функция не имеет точек перегиба - она просто вогнутая - ОТВЕТ
Подтверждается графиком функции и производных.