Вначале сделаем некоторые упрощения (основные свойства корней и степеней, фактически никаких подсчетов):
![\displaystyle 0,6^{\frac{1}{3} } \cdot 1,3 ^{- \frac{2}{5} } = \sqrt[3]{0,6^1} \cdot \frac{1}{1,3 ^ \frac{2}{5} } = \sqrt[3]{0,6} \cdot \frac{1}{ \sqrt[5]{1,3^2} } = \sqrt[3]{0,6} \cdot \sqrt[5]{\frac{1}{{1,3^2} } } =\\\\= \sqrt[15]{0,6^5} \cdot \sqrt[15]{\frac{1^3}{1,3^6 } } = \sqrt[15]{ \frac{0,6^5}{1,3^6} }](/tpl/images/1356/7357/cd94e.png)
А теперь можно либо посчитать, что находится под корнем, либо избежать муторных вычислений и сразу сказать, что числитель меньше знаменателя, и дробь меньше единицы. Значит, и корень из такой дроби тоже меньше единицы.
Итог: число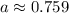 
не подходит.
Расписываю менее подробно:
![\displaystyle 0,7^{- \frac{2}{3} } \cdot 0,3^{- \frac{1}{5} } = \sqrt[3]{\frac{1}{0,7^2} } \cdot \sqrt[5]{\frac{1}{0,3^1} } = \sqrt[15]{\frac{1}{0,7^{10}} } \cdot \sqrt[15]{\frac{1}{0,3^3} } = \sqrt[15]{ \frac{1}{0,7^{10} \cdot 0,3^3} }](/tpl/images/1356/7357/048b4.png)
Очевидно, что знаменатель в подкоренном выражении меньше единицы, поэтому само подкоренное выражение больше единицы. И корень больше единицы.
Итог: число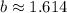 
подходит.
3). Третье число.
И, наконец, последнее число:
![\displaystyle 1,8^{\frac{1}{3} } \cdot 0,3^{-\frac{2}{5} } = \sqrt[3]{1,8} \cdot \sqrt[5]{\frac{1}{0,3^2} } = \sqrt[15]{1,8^5} \cdot \sqrt[15]{\frac{1}{0,3^6} } = \sqrt[15]{ \frac {1,8^5}{0,3^6} }](/tpl/images/1356/7357/0ad66.png)
Здесь, опять, подкоренное выражение больше единицы (по вполне понятным причинам), так что и сам корень будет больше единицы.
Итог: число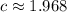 
подходит.
Пошаговое объяснение:
1. Мы находимся в условиях "испытаний Бернулли", где "опытом" является выбор отдельной кошки, а "событием" - факт кражи еды данной кошкой. Число "опытов" по условию равно 243, вероятность p появления "события" в одном "опыте" равна p=3/4=0,75, вероятность непоявления события q=1-p=0,25. Тогда вероятность P того, что в серии из n=243 опытов событие появится m=122 раза, равна P=C(n,m)*p^m*q^(n-m), где C(n,m) - число сочетаний из n по m. Однако так как число "опытов" велико и при этом произведение n*p*q>10, то для приближённого вычисления вероятности P можно использовать локальную формулу Лапласа:
P≈e^(-x²/2)/√(2*π*n*p*q), где x=(m-n*p)/√(n*p*q).
Подставляя в эту формулу известные данные, находим P≈0,0000000000000000003≈0.
2. Для вычисления вероятности P используем интегральную формулу Лапласа: P≈Ф(x2)-Ф(x1), где Ф(x) - функция Лапласа, x1=(m1-n*p)/√(n*p*q), x2=(m2-n*p)/√(n*p*q). Так как по условию m1=100 и m2=200, то, находя x1, x2 и вычисляя затем Ф(x1) и Ф(x2), находим P≈0,9957.
3. Задача решается аналогично задаче п.2. Меньше 180 кошек - это значит от 0 до 179 кошек, поэтому в данном случае m1=0 и m2=179. Находя x1, x2 и вычисляя затем Ф(x1) и Ф(x2), находим P≈0,3151.
4. Задача также решается аналогично задаче п.2, только в данном случае m1=51 и m2=243. Находя x1, x2 и вычисляя затем Ф(x1) и Ф(x2), находим P≈1.
с[c]-согл.,глух.,твёрд.,парный
п[п]-согл.,глух.,твёрд.,парный
а[а]-гл.
с[с]-согл.,глух.,твёрд.,парный
а[а]-гл.
ю[й']-согл., звон., мягк., непарный
[у] -гл.
т[т]-согл.,глух.,твёрд.,парный
Букв: 7
Звуков: 8