Пошаговое объяснение:
1)Все многоугольники имеют хотя бы три вершины - верно
2)Некоторые четырехугольники имеют пять вершин - неверно , поскольку четырехугольник имеет только 4 вершины
3)Все прямоугольники квадраты - неверно, у прямоугольника противоположные стороны равны , а у квадрата все стороны равны
4)Некоторые квадраты не прямоугольники - неверно, все квадраты прямоугольники
5)Все четырехугольники, у которых имеется два прямых угла, - прямоугольники - неверно
6)Существуют четырехугольники, у которых имеется хотя бы один прямой угол - верно
7)Существуют треугольники, у которых имеется хотя бы два тупых угла- неверно , сумма всех углов в треугольнике равна 180°, а если 2 угла будут тупыми , то сумма всех углов будет больше 180°
ответ : истинные высказывания 1 и 6
(см. объяснение)
Пошаговое объяснение:
Вынесении общего множителя за скобки.
Рассмотрим пример:
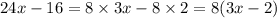
Хорошо видно, что и 24 и 16 делятся на 8. Тогда 8 - это общий множитель, который можно вынести за скобки. Далее делим исходное выражение на 8 и отправляем полученное в скобки.
Попробуйте решить самостоятельно:
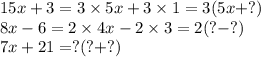
(ответы в конце объяснения)
Вынесении многочлена за скобки:
Прием тут аналогичен описанному выше.
Рассмотрим пример:
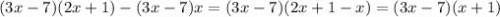
Здесь все то же самое, только за скобки выносится общая часть.
При этом не нужно бояться выражения в скобках!
Если оно одинаково, то смело пользуйтесь приемом:
![(\sqrt[7]{x}+\arcsin (x))(\cos(x)+\sqrt[7]{x})-(\sqrt[7]{x}+\arcsin (x))^2=\\=(\sqrt[7]{x}+\arcsin (x))(\cos(x)+\sqrt[7]{x}-(\sqrt[7]{x}+\arcsin (x)))=\\=(\sqrt[7]{x}+\arcsin (x))(\cos(x)-\arcsin (x))](/tpl/images/1643/8776/95ae2.png)
Каким бы страшным не показалось семикласснику это выражение, прием остается 100% таким же!
Группировка.
Рассмотрим пример:
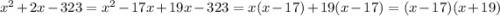
Здесь необходимо представить 2x, как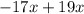 
. После чего воспользоваться знаниями выше.
Иногда сразу дают выражение вида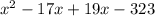 
, что упрощает ситуацию.
ответы к заданиям для самостоятельного решения.
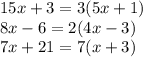
Объяснение завершено!
ответ:5 билетов