Пошаговое объяснение:
а) Может, например: 1009 ; 10 ; 1
б ) Нет , потому что число и сумма его цифр имеют равные остатки при делении на 3, а значит, сумма этих трёх чисел должна быть кратна 3.
в ) Последнее равно 3, значит, 2 число равно 12 или 21.
Цифры, сумма которых равна 12:
12 = 0+3+9 = 0+4+8 = 0+5+7 = 0+6+6 = 1+2+9 = 1+3+8 = 1+4+7 = 1+5+6 =
= 2+2+8 = 2+3+7 = 2+4+6 = 2+5+5 = 3+3+6 = 3+4+5
Теперь считаем.
Из цифр 039, 048, 057 можно сложить по 4 числа. Всего 3*4 = 12 чисел.
Из 066 можно сложить 2 числа: 606 и 660.
Из 3 разных цифр можно сложить по 6 чисел. Всего 7*6 = 42 числа.
Из цифр 228, 255, 336 можно сложить по 3 числа. Всего 3*3 = 9 чисел.
Всего 12 + 2 + 42 + 9 = 65 троек.
Цифры, сумма которых равна 21:
21 = 3+9+9 = 4+8+9 = 5+7+9 = 5+8+8 = 6+7+8 = 7+7+7
Из цифр 399 и 588 можно сложить по 3 числа. Всего 3*2 = 6 чисел.
Из 3 разных цифр можно сложить по 6 чисел. Всего 3*6 = 18 чисел.
Число 777 - только 1 число.
Всего 6 + 18 + 1 = 25 троек.
Итого получается 65 + 25 = 90 троек.
В 4-е раза.
Пошаговое объяснение:
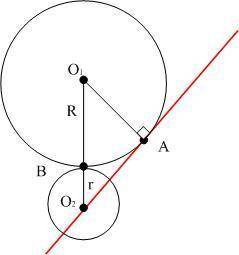
Условие с обозначениями на риунке, и IAO₂I=3r
Итак, запишем вопрос задачи формально:
2πR/(2πr)=R/r;
задача заключаетс в нахождении онтошения радиусов окружностей.
Приступим.
Рассмотрим Δ О₁АО₂. Его угол ∠О₁АО₂=90° (по определению касательной и угла в точке касания).
По теореме Пифагора для этого треугольника запишем:
IO₁O₂I=√(IO₁AI²+IO₂AI²); (1)
Но с другой стороны IO₁O₂I=R+r (по свойству точки касания окружностей; точка касания лежит на отрезке, соединяющем центры этих окружностей).
IO₁AI²=R; IO₂AI²=3r (по условию)
Перепишем первое равенство:
R+r=√(R²+(3r)²); (2)
Решаем уравнение (2):
(R+r)²=√(R²+(3r)²)²;
R²+2Rr+r²=R²+9r²;
R²+2Rr+r²-R²-9r²=0;
Приводим подобные, выносим общие множители:
2Rr-8r²=0;
2r(R-4r)=0;
2r=0 - не подходит!
R-4r=0;
R=4r;
R/r=4.