ответ г) 8
Пошаговое объяснение:
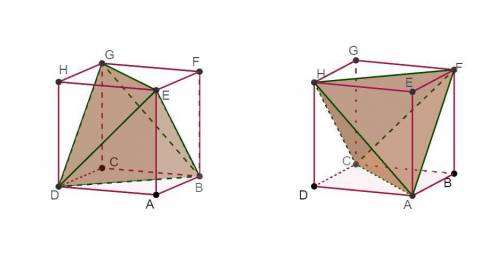
Три вершины куба принадлежат плоскости, проходящей через диагонали трех смежных граней куба.
Плоскости, проходящие через 3 вершины куба, образуют вписанный в куб правильный тетраэдр.
Правильный тетраэдр можно вписать в куб двумя так как каждая грань куба имеет две диагонали.
Ребро одного тетраэдра пройдет по одной диагонали данной грани куба, а ребро второго тетраэдра пройдет по другой диагонали данной грани куба.
Каждый из двух тетраэдров имеет по 4 грани, образованных четырьмя плоскостями.
Всего 8 плоскостей будут проходить через 3 вершины куба. ответ г) 8.
Рисунок в приложении.
12/(х^2-2х+3)=х^2-2х-1
x^2-2x+1=t
12/(t+2)=t-2
12=t^2-4
t^2=16
t1=4
t2=-4
x^2-2x+1=4
x^2-2x-3=0
D=4+12=16=4^2
x1=(2+4)/2=3
x2=(2-4)/2=-1
x^2-2x+1=4
(x-1)^2=-4 Квадрат числа не может быть < 0
ответ: 3; -1