Дано :
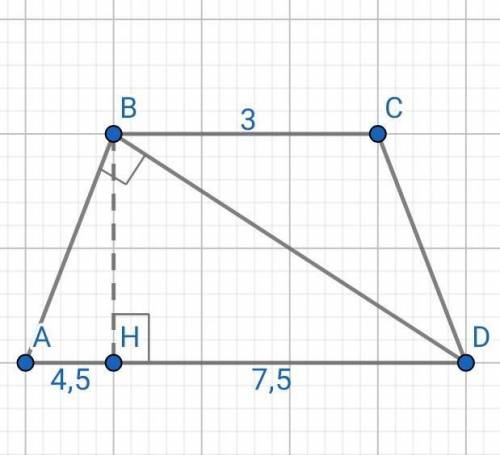
ABCD - равнобедренная трапеция
ВС = 3, AD = 12 (основания)
ВН - высота
<ABD = 90°.
Найти :
Длину диагонали = ?
ВН = ?
АВ = ?
Рассмотрим прямоугольный треугольник ABD.
Так как высота ВН проведена г гипотенузе треугольника (это такая сторона, лежащая против угла в 90°), то по свойству пропорциональных отрезков в прямоугольном треугольнике :
ВН² = АН*HD.
Отрезок АН находим по свойству отрезков в равнобедренной трапеции, образованных основанием высоты :
АН = (AD - BC)/2 = (12-3)/2 = 9/2 = 4,5.
HD = AD - AH = 12 - 4,5 = 7,5.
BH = √(4,5*7,5) = √33,75.
===
Теперь находим боковую сторону и длину диагонали.
Нам достаточно будет найти только длину диагонали DB, так как в равнобедренной трапеции диагонали равны, и смысла искать отрезок АС не имеет.
AB = √(AH*AD) = √(4,5*12) = √54.
DB = √(HD*AD) = √(7,5*12) = √90.
√90, √33,75, √54.
ответ: 180°-a
Раз уж нарисовал рисунок, все таки добавлю ответ
Пошаговое объяснение:
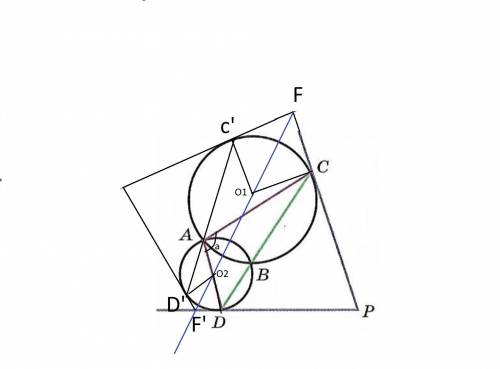
Отразим картинку относительно линии соединяющей центры окружностей ( как показано на рисунке). По принципу того, что вписанный в угол окружность вдвое меньше центрального имеем
∠CO1C' = 2∠CAC'
∠DO2D'=2∠DAD'
∠CO1C' + ∠DO2D' = 2∠CAC' + 2∠DAD' =2*(180° -a) = 360°-2a
Поскольку касательные перпендикулярны радиусам, то два из углов каждого из четырехугольников O1C'FC и O2D'F'D равны по 90°, а сумма углов в обоих четырехугольниках 720°, то
∠CFC' +∠DF'D' = 720° - 90°*4 - (360°-2a) = 2a
Из симметрии картинки ясно, что ∠PFF'+∠PF'F = (∠CFC' +∠DF'D')/2 = a
Таким образом, из суммы углов ΔPFF' имеем :
∠P = 180° -∠PFF'+∠PF'F = 180°-a
...