Назовем множество девочек  , а множество мальчиков --
, а множество мальчиков --  . Социальную группу назовем примитивной, если удаление любого мальчика из нее сделает группу не социальной. Тем самым, всякая социальная группа порождена некоторой примитивной. Пусть
. Социальную группу назовем примитивной, если удаление любого мальчика из нее сделает группу не социальной. Тем самым, всякая социальная группа порождена некоторой примитивной. Пусть  -- число продолжений примитивной социальной группы
-- число продолжений примитивной социальной группы 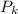 . Ясно, что
. Ясно, что 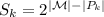 , поскольку объединение любого подмножества с социальной группой дает социальную группу. Количество социальных групп тем самым равно
, поскольку объединение любого подмножества с социальной группой дает социальную группу. Количество социальных групп тем самым равно 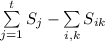 , где
, где 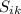 -- число продолжений социальной группы
-- число продолжений социальной группы 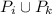 . В самом деле, когда мы считаем число продолжений, мы не должны забывать, что у двух примитивных социальных групп может быть одинаковое продолжение. Если продолжения групп
. В самом деле, когда мы считаем число продолжений, мы не должны забывать, что у двух примитивных социальных групп может быть одинаковое продолжение. Если продолжения групп 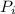 и
и 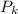 совпадают, то они обязательно содержат
совпадают, то они обязательно содержат 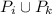 . Договоримся называть пустое множество примитивной социальной группой. Тогда если в первой сумме
. Договоримся называть пустое множество примитивной социальной группой. Тогда если в первой сумме  для некоторого
для некоторого 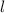 , то перенесем это значение (без ущерба для четности) во вторую сумму, считая эту величину числом продолжений группы
, то перенесем это значение (без ущерба для четности) во вторую сумму, считая эту величину числом продолжений группы 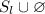 . Имеем тогда: первая сумма есть четное число, а слагаемое во второй сумме является нечетным тогда и только тогда, когда
. Имеем тогда: первая сумма есть четное число, а слагаемое во второй сумме является нечетным тогда и только тогда, когда 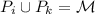 .
.
Утверждение: число пар примитивных множеств 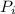 и
и 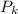 таких, что
таких, что 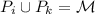 имеет ту же четность, что и количество пар аналогичных множеств для
имеет ту же четность, что и количество пар аналогичных множеств для 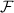 .
.
Доказательство: в качестве доказательства можно посмотреть на иллюстрацию, где, например, 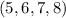 и
и 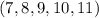 -- социальные. Теперь построим естественное соответствие. Из каждой вершины отметим ненулевое количество красных и синих ребер (иногда одно ребро красится двумя цветами). Тогда "образы" точек под действием красных ребер дадут социальную группу, скажем,
-- социальные. Теперь построим естественное соответствие. Из каждой вершины отметим ненулевое количество красных и синих ребер (иногда одно ребро красится двумя цветами). Тогда "образы" точек под действием красных ребер дадут социальную группу, скажем, 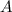 , а под действием синих --
, а под действием синих -- 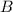 (причем
(причем 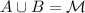 ). Теперь сотрем цвета и сделаем аналогичную раскраску, но для множества
). Теперь сотрем цвета и сделаем аналогичную раскраску, но для множества 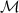 (то есть для ребер, исходящих из множества мальчиков). Здесь уже будет гарантироваться, что объединение социальных групп в множестве девочек будет давать
(то есть для ребер, исходящих из множества мальчиков). Здесь уже будет гарантироваться, что объединение социальных групп в множестве девочек будет давать 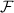 . Количество таких раскрасок -- четное число (в вершинах степени не меньше
. Количество таких раскрасок -- четное число (в вершинах степени не меньше 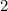 число вариантов четно; случай, когда таких нет рассмотрим отдельно), а потому общее число пар четно. Симметрично рассматривается количество пар в
число вариантов четно; случай, когда таких нет рассмотрим отдельно), а потому общее число пар четно. Симметрично рассматривается количество пар в 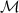 . Ключевое здесь то, что оба множества покрывают друг друга ребрами.
. Ключевое здесь то, что оба множества покрывают друг друга ребрами.
Если все степени вершин равны  (например, в
(например, в 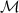 ), то имеется единственный случай: когда берется объединение
), то имеется единственный случай: когда берется объединение 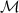 и пустого множества. Но ребра из
и пустого множества. Но ребра из 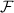 накрывают
накрывают 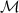 (поскольку ребер нулевой степени нет), а потому и в
(поскольку ребер нулевой степени нет), а потому и в 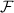 есть такая пара. ∵
есть такая пара. ∵
Получили, что четность 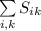 совпадает в обоих множествах, а значит, совпадает и четность всей суммы.
совпадает в обоих множествах, а значит, совпадает и четность всей суммы.
прощения, что так мудрено. Если что, отвечу на вопросы.