Математика: Решить уравнения.1) 7x=0. 2) 7x=1. 3) (x+3)(x+7)= 0.

Решить уравнения.1) 7x=0. 2) 7x=1. 3) (x+3)(x+7)= 0.

👇

Увидеть ответ

Ответ:

Дмитртй11

04.05.2023

1) 7х = 0 ; х = 0
2) 7х = 1 ; х = 1/7
3) (х + 3)(х + 7) = 0 ; (х + 3) = 0 ; х = - 3 ; (х + 7) = 0 ; х = - 7

4,8(55 оценок)

Ответ:

ReginaRem27

04.05.2023

7х=0
х=0

7х=1
х=1/7

(х+3)(х+7)=0
х=-3
х=-7

4,8(97 оценок)

Открыть все ответы

Ответ:

голозавр

04.05.2023

Пошаговое объяснение:

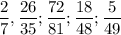
$\displaystyle \frac{2}{7} , \frac{26}{35}; \frac{72}{81}; \frac{18}{48} ; \frac{5}{49}$

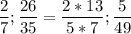дроби $\displaystyle \frac{2}{7} ; \frac{26}{35}= \frac{2*13}{5*7} ; \frac{5}{49}$ несократимые, поскольку числитель и знаменатель этих дробей - взаимно простые числа , то есть имеют единственный общий положительный делитель, равный единице.

дробь 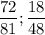$\displaystyle \frac{72}{81 } ; \frac{18}{48}$ можно сократить

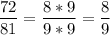
$\displaystyle \frac{72}{81}= \frac{8*9}{9*9}= \frac{8}{9}$

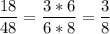
$\displaystyle \frac{18}{48}= \frac{3*6}{6*8}= \frac{3}{8}$

Получаем дроби :

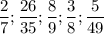
$\displaystyle \frac{2}{7} ; \frac{26}{35} ; \frac{8}{9} ; \frac{3}{8} ; \frac{5}{49}$

Найдем общий знаменатель для этих дробей , для этого найдем НОК ( 7;8;9;35;49)

Разложим числа на простые множители. Сначала запишем разложение на множители наибольшего число, затем остальные числа.

49= 7*7

35 = 5 *7

7 = 7

8 = 2 *2* 2

9 = 3 *3

Чтобы определить НОК, необходимо недостающие множители (эти множители подчеркнуты) добавить к множителям большего числа и перемножить их:

НОК (7; 8; 9; 35) = 7* 7*5* 2 * 2 * 2 * 3 * 3 = 17640

Общий знаменатель будет 17640 , значит получим ряд дробей :

$\displaystyle \frac{2}{7}= \frac{2* 2520}{7*2520}= \frac{5040}{17640}\\ \\ \\ \frac{26}{35}= \frac{26*504}{504*35}= \frac{13104}{17640}\\ \\ \\ \frac{8}{9}= \frac{8*1960}{9*1960}= \frac{15680}{17640}\\ \\ \\ \frac{3}{8}= \frac{3*2205}{8*2205}= \frac{6615}{17640} \\ \\ \\ \frac{5}{49}= \frac{5*360}{49*360}= \frac{1800}{17640}$

В ряду дробей с одинаковым знаменателем большей будет та у которой числитель больший . Упорядочим наш ряд :

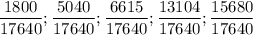
$\displaystyle \frac{1800}{17640} ; \frac{5040}{17640} ; \frac{6615}{17640} ; \frac{13104}{17640} ; \frac{15680}{17640}$

Значит первоначальный ряд в порядке возрастания будет :

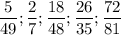
$\displaystyle \frac{5}{49} ; \frac{2}{7} ; \frac{18}{48} ; \frac{26}{35} ; \frac{72}{81}$

2) Решаем по тому же алгоритму

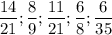
$\displaystyle \frac{14}{21} ; \frac{8}{9} ; \frac{11}{21} ; \frac{6}{8} ; \frac{6}{35}$

Несократимые дроби : 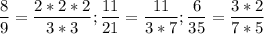$\displaystyle \frac{8}{9}= \frac{2*2*2}{3*3} ; \frac{11}{21}= \frac{11}{3*7} ; \frac{6}{35}= \frac{3*2}{7*5}$

Сократимые :

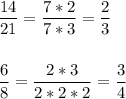
$\displaystyle \frac{14}{21}= \frac{7*2}{7*3}= \frac{2}{3}\\ \\ \\ \frac{6}{8}= \frac{2*3}{2*2*2}= \frac{3}{4}$

Получили ряд дробей :

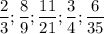
$\displaystyle \frac{2}{3} ; \frac{8}{9} ; \frac{11}{21} ; \frac{3}{4} ; \frac{6}{35}$

Найдем общий знаменатель , а для этого найдем

НОК ( 3;4;9;21;35)

35 = 5*7

21= 3*7

9= 3*3

4= 2*2

3= 3*1

НОК ( 3;4;9;21;35) = 5*7*3*3*2*2= 1260 - это и будет общий знаменатель

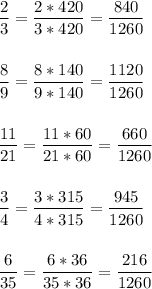
$\displaystyle \frac{2}{3}= \frac{2*420}{3*420}= \frac{840}{1260}\\ \\ \\ \frac{8}{9}= \frac{8*140}{9*140} = \frac{1120}{1260}\\ \\ \\ \frac{11}{21}= \frac{11*60}{21*60}= \frac{660}{1260}\\ \\ \\ \frac{3}{4}= \frac{3*315}{4*315}= \frac{945}{1260}\\ \\ \\ \frac{6}{35}= \frac{6*36}{35*36}= \frac{216}{1260}$

Упорядочим ряд по возрастанию :

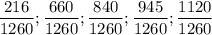
$\displaystyle \frac{216}{1260} ; \frac{660}{1260} ; \frac{840}{1260} ; \frac{945}{1260} ; \frac{1120}{1260}$

Соответственно , первоначальный ряд в порядке возрастания будет

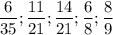
$\displaystyle \frac{6}{35} ; \frac{11}{21} ; \frac{14}{21} ; \frac{6}{8} ; \frac{8}{9}$

4,6(51 оценок)

Ответ:

1256545544

04.05.2023

Илонская башня не входит в «официальный» список чудес света. Однако она — одно из самых выдающихся сооружений Древнего Вавилона, а ее название и поныне является символом сумятицы и беспорядка. Сюжет о Вавилонской башне распространён в христианской иконографии — в многочисленных миниатюрах, рукописных и печатных изданиях Библии (например, в миниатюре английской рукописи XI века); а также в мозаиках и фресках соборов и церквей (например, мозаика собора Сан-Марко в Венеции, конец XII — начало XIII в.).

В европейской живописи наиболее знаменитой картиной на этот сюжет является полотно Питера Брейгеля Старшего «Вавилонское столпотворение» (1563). Более стилизованное геометрически сооружение изобразил М. Эшер на гравюре 1928 года.

4,6(20 оценок)

Это интересно:

Кулинария-и-гостеприимство

02.05.2023

Как сварить овощи: простые рецепты и полезные советы...

Кулинария-и-гостеприимство

24.06.2022

Как приготовить курицу с рисом: пошаговый рецепт для начинающих...

Кулинария-и-гостеприимство

25.08.2021

Как сделать чай из роз: полезные рецепты и особенности приготовления...

Искусство-и-развлечения