(см. объяснение)
Пошаговое объяснение:
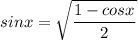
Преобразуем выражение:
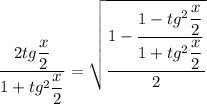
Теперь можно заменить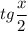 
на t:
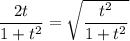
Решим это уравнение:
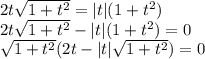
Знаем, что произведение равно 0, если хотя бы 1 из его множителей равен 0, а другой при этом не теряет смысла.
Тогда:
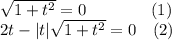
Рассмотрим первое уравнение:
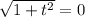
Выражение равно 0, если подкоренное выражение равно 0.
Тогда:
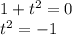
У уравнения нет корней.
Рассмотрим второе уравнение:
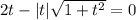
Раскроем модуль:
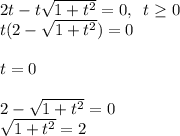
Поскольку обе части положительны, можно возводить их в квадрат:
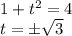
Т.к.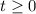 
, - корень из 3 не подходит.
При t<0:
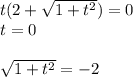
Подкоренное выражение не может быть равно -2, поэтому уравнение корней не имеет.
Т.к. t<0, то корень 0 посторонний.
Итого:
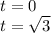
Выполним обратную замену:
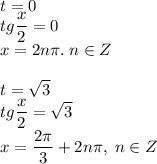
Уравнение решено!
Перейдем к отбору корней:
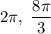
Отбор корней выполнен!
(см. объяснение)
Пошаговое объяснение:
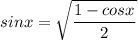
Преобразуем выражение:
Теперь можно заменить 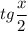на t:
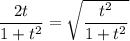
Решим это уравнение:
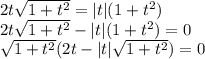
Знаем, что произведение равно 0, если хотя бы 1 из его множителей равен 0, а другой при этом не теряет смысла.
Тогда:
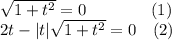
Рассмотрим первое уравнение:
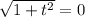
Выражение равно 0, если подкоренное выражение равно 0.
Тогда:
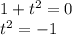
У уравнения нет корней.
Рассмотрим второе уравнение:
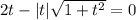
Раскроем модуль:
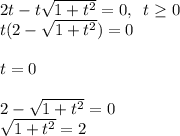
Поскольку обе части положительны, можно возводить их в квадрат:
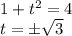
Т.к. 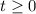, - корень из 3 не подходит.
При t<0:
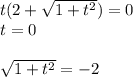
Подкоренное выражение не может быть равно -2, поэтому уравнение корней не имеет.
Т.к. t<0, то корень 0 посторонний.
Итого:
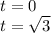
Выполним обратную замену:
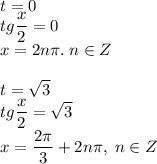
Уравнение решено!
Перейдем к отбору корней:
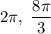
Отбор корней выполнен!
Решено.