Привет! Сейчас все запишем:
1) Подставим значение у формулу:
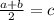
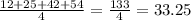
2) C даной формулы видно, что мы делим сумму чисел на количество чисел.
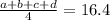
Значит, если мы помножим все и вся на 4, тогда у нас получится сумма этих чисел:
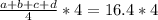
a+b+c+d=65,6
3) Воспользуемся предыдущей формулой:
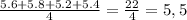
4) Процент числа - это умножение на 100 (%) по этому, чтобы нам получить десятичную дробь нужно поделить на 100:
1.75/100=0.0175
5) Сделаем соотношение, где Х - масса бананов:
2400 кг - 100%
Х кг - 12%
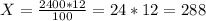
Масса бананов - 288 кг
6) Сделаем соотношение, где Х - вся сумма (грн):
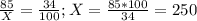
Вся сумма - 250 грн
7) Запишем вес дынь: 2 по 2.4 кг , 4 по 2.8 кг, 6 по 2.2 кг . 2+4+6=12 дынь. Значит остались 8 дынь по 2.3 кг (20-12=8)
Найдем их среднее арифметическое:
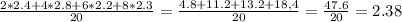
2.38≅2.4 . ответ: 2.4 кг
8) I. Найдем количество кустиков малины, для этого сделаем соотношение:
60 кустиков - 100%
Х кустиков - 35%
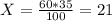
X=количество кустиков малины = 21 кустик
II. Нам сказали, что 21 кустик малины - это только 70 % кустиков смородины. Делаем соотношение, где Y - кустики смородины
21 кустик - 70%
Y - кустиков - 100%
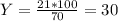
Значит у нас 30 кустиков смородины
III. Найдем количество кустиков крыжовника:
60-30-21=9 кустиков
9) I. Найдем корень уравнение:
2,6x - 3,3x + 4,6x = 78
3.9 х = 78
x=78/3.9=20
II. Сделаем соотношение:
20 - 100%
X - 20%
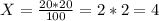
10) I. Сделаем соотношение:
9 рыбок - 30%
Х рыбок - 100%
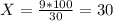
Значит весь улов - 30 рыбок
II. Найдем среднее арифметическое (сколько рыбок он поймал в среднем за один час).
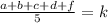
a+b+c+d+f = 30, ибо это количество рыбы. А 5 - это количество времени, которое он провел на рыбалке.
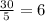
ответ: в среднем 6 рыбок
Готово! Есть вопросы? Напишите, с радостью отвечу на них
*Поставьте лучшее
![t^2 - 8 t + [7-a] = 0 ,](/tpl/images/0495/7941/4dac0.png) где под
где под 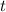 подразумевается квадрат переменной
подразумевается квадрат переменной 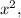 т.е.
т.е.  а его корнями
а его корнями 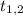 – квадраты искомых корней, если они различны, или его чётным корнем
– квадраты искомых корней, если они различны, или его чётным корнем 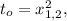 если корень биквадратного трёхчлена
если корень биквадратного трёхчлена 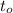 – единственный.
– единственный.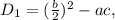 тогда
тогда ![D_1 = 4^2 - [7-a] = 9 + a .](/tpl/images/0495/7941/d229f.png) Потребуем, чтобы
Потребуем, чтобы 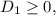 откуда следует, что
откуда следует, что 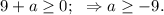
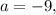 а корень биквадратного трёхчлена станет чётным
а корень биквадратного трёхчлена станет чётным  давая два искомых корня
давая два искомых корня 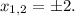 Это значение
Это значение 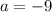 как раз уже и есть одно из искомых решений для параметра
как раз уже и есть одно из искомых решений для параметра 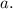
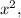 всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней
всегда будет два – левый и правый (меньший и больший), однако при некоторых обстоятельствах левый квадрат искомых корней будет отрицательным, а значит, не будет давать пару искомых корней. Среднеарифметическое квадратов искомых корней 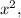 по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно
по теореме Виета, в применении к биквадратному уравнению, будет равно числу, противоположному половине среднего коэффициента, т.е. оно равно 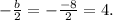 Отсюда следует, что правый квадрат искомых корней
Отсюда следует, что правый квадрат искомых корней 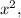 – всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.
– всегда положителен, а значит, всегда даёт два корня при положительном дискриминанте.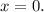 А значит, значение всего трёхчлена
А значит, значение всего трёхчлена ![x^4 - 8 x^2 + [7-a]](/tpl/images/0495/7941/7bbf9.png) взятое от
взятое от 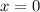 должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.
должно давать отрицательное значение, т.е. располагается в нижней межкорневой дуге параболы биквадратного трёхчлена.![0^4 - 8 \cdot 0^2 + [7-a] < 0](/tpl/images/0495/7941/13440.png) ;
; ;
;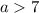 ;
;
(A xor B) and C или (A <> B) and C
в терминах V /\ ¬
((¬A /\ B) V (A /\ ¬B)) /\ C