Question

Х^2+10х+11> 0 ; х^2-3х+2≥0 развязать неравенство (х-2,5)(х+4)≤0 ; х(х+3,2)> 0 развязать неравенство аналитичным х+4)(х+5,6)< 0 ; х(х-5)(х+5)≥0 развязать неравенство методом интервалов ! заранее )

Answer 1

$x^2+10x+11\ \textgreater \ 0, \\ x^2+10x+11=0, \\ D_{/4}=5^2-11=14, \\ x=-5\pm\sqrt{14}, \\ \begin{array}{c|ccccc}x&(-\infty;-5-\sqrt{14})&-5-\sqrt{14}&(-5-\sqrt{14};-5-\sqrt{14})&-5+\sqrt{14}&(-5+\sqrt{14};+\infty)\\x^2+10x+11&+&0&-&0&+\end{array} \\ (x+5+\sqrt{14})(x+5-\sqrt{14})\ \textgreater \ 0, \\ x\in(-\infty;-5-\sqrt{14})\cup(-5+\sqrt{14};+\infty).$

$x^2-3x+2\geq0; \\ x^2-3x+2=0;, \\ x_1=1, \ x_2=2, \\ (x-1)(x-2)\geq0, \\ \begin{array}{c|ccccc}x&(-\infty;1)&1&(1;2)&2&(2;+\infty)\\x^2-3x+2&+&0&-&0&+\end{array} \\ \\ (-\infty;1]\cup[2;+\infty)$

$(x-2,5)(x+4)\leq0; \\ \left [ {{ \left \{ {{x-2,5 \leq 0,} \atop {x+4 \geq 0,}} \right. } \atop { \left \{ {{x-2,5 \geq 0,} \atop {x+4 \leq 0;}} \right. }} \right. \left [ {{ \left \{ {{x \leq 2,5,} \atop {x \geq -4,}} \right. } \atop { \left \{ {{x \geq 2,5,} \atop {x \leq -4;}} \right. }} \right. \left [ {{-4 \leq x \leq 2,5,} \atop {x\in\varnothing;}} \right. \\ -4 \leq x \leq 2,5, \\ x\in[-4;2,5].$

$x(x+3,2)\ \textgreater \ 0; \\ \left [ {{ \left \{ {{x \ \textless \ 0,} \atop {x+3,2\ \textless \ 0,}} \right. } \atop { \left \{ {{x\ \textgreater \ 0,} \atop {x+3,2\ \textgreater \ 0;}} \right. }} \right. \left [ {{ \left \{ {{x \ \textless \ 0,} \atop {x\ \textless \ -3,2,}} \right. } \atop { \left \{ {{x \ \textgreater \ 0,} \atop {x\ \textgreater \ -3,2;}} \right. }} \right. \left [ {{x\ \textless \ -3,2,} \atop {x\ \textgreater \ 0;}} \right. \\x\in(-\infty;-3,2)\cup(0;+\infty).$

$(x+4)(x+5,6)\ \textless \ 0; \\ (x+4)(x+5,6)=0, \\ x_1=-5,6, \ x_2=-4; \\ \begin{array}{c|ccccc}x&(-\infty;-5,6)&-5,6&(-5,6;-4)&-4&(-4;+\infty)\\(x+4)(x+5,6)&+&0&-&0&+\end{array} \\ \\ x\in(-5,6;-4).$

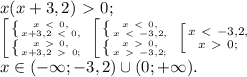
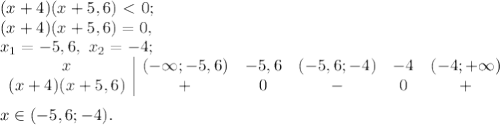
$x(x-5)(x+5) \geq 0; \\ x(x-5)(x+5)=0, \\ x_1=-5, \ x_2=0, \ x_3=5 \\ \begin{array}{c|ccccccc}x&(-\infty;-5)&-5&(-5;0)&0&(0;5)&5&(5;+\infty)\\x(x-5)(x+5)&-&0&+&0&-&0&+\end{array} \\ \\ x\in[-5;0]\cup[5;+\infty).$