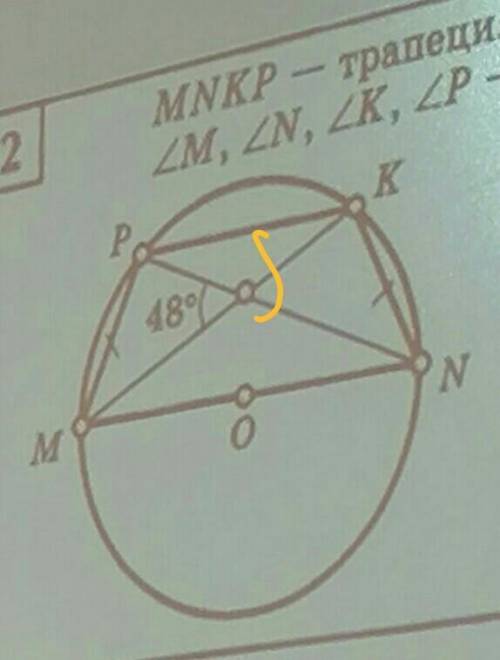
Угол MPN= 90°,т.к опирается на диаметр MN.
Рассматривая треугольник MPS, где угол MPS=90°, угол MSP=48°, следовательно угол PMS= 42°.
Угол KSN=PSM(как вертикальные)
Угол MKN=MPN(т.к опираются на MN.
Значит, угол KNP=42°.
Угол MSN= 180°-угол PSM= 180°-48= 132°
MS=SN( в равнобедренной трапеции диагонали делятся точкой пересечения на попарно равные отрезки)=> треугольник MSN - равнобедренный.
угол SMN+угол SNM= 180°- угол MSN= 180°-132°=48°
угол SMN=углу SNM= 48°/2= 24°
Следовательно угол М=угол PMS+ угол SMN= 42°+24°= 66°
Угол N=углу М= 66°(т.к равнобедренная трапеция)
Угол P= 180°- угол М= 114°
Угол К= углу P= 114°.
ответ: Угол М,N= 66°; угол P,K= 114°.
функции: f(x) = x^2 - 3x + 1.
Воспользовавшись основными формулами дифференцирования и правилами дифференцирования:
(x^n)’ = n * x^(n-1).
(с)’ = 0, где с – const.
(с * u)’ = с * u’, где с – const.
(u ± v)’ = u’ ± v’.
y = f(g(x)), y’ = f’u(u) * g’x(x), где u = g(x).
Таким образом, производная нашей данной функции будет следующая:
f(x)' = (x^2 - 3x + 1)’ = (x^2)’ – (3x)’ + (1)’ = 2 * x^(2 – 1) – 3 * x^(1 - 1) – 0 = 2x – 3.
ответ: Производная нашей данной функции будет равна f(x)' = 2x – 3.
Пошаговое объяснение:
надеюсь
t2=x+1/6
Составим уравнение:
66х=(х+1/6)×60
66х=60х+10
6х=10
х=10/6=5/3=1 ⅔
Тогда расстояние равно 1⅔×66=110 км.
Проверим t2=10/6 + 1/6=11/6. S=11/6 × 60 =110
ответ: а) 110 км