ответ: sin x/2+cos x/2=√(1 -2√10/11)
Пошаговое объяснение:
sinx/2+cosx/2, если cosx=−9/11 и x∈(π;3π/2)
1) (sin x/2+cos x/2)²=sin²(x/2) + 2· sin(x/2)·cos(x/2) + cos²(x/2) =sin²(x/2) + cos²(x/2) + 2· sin(x/2)·cos(x/2) =1 + 2· sin(x/2)·cos(x/2) = 1+sin x
2) если cosx=−9/11 и x∈(π;3π/2), то
sin²x=1-cos²x = 1 - (-9/11)²= 1 - 81/121 =40/121 ⇒sin x=±√40/121=±2√10/11
Но х∈ 3 четверти, т.к. x∈(π;3π/2), значит sin x<0, т.е.
sin x= - 2√10/11
3) (sin x/2+cos x/2)²=1+sin x = 1 -2√10/11 ⇒ x/2 ∈(π/2 ; 3π/4)
sin x/2+cos x/2=√(1 -2√10/11)
рис 1:
Для вычисления обратной матрицы запишем матрицу А, дописав к ней справа единичную матрицу:
Теперь чтобы найти обратную матрицу, используя элементарные преобразования над строками матрицы, преобразуем левую часть полученной матрицы в единичную.
от 2 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 2
рис 2:
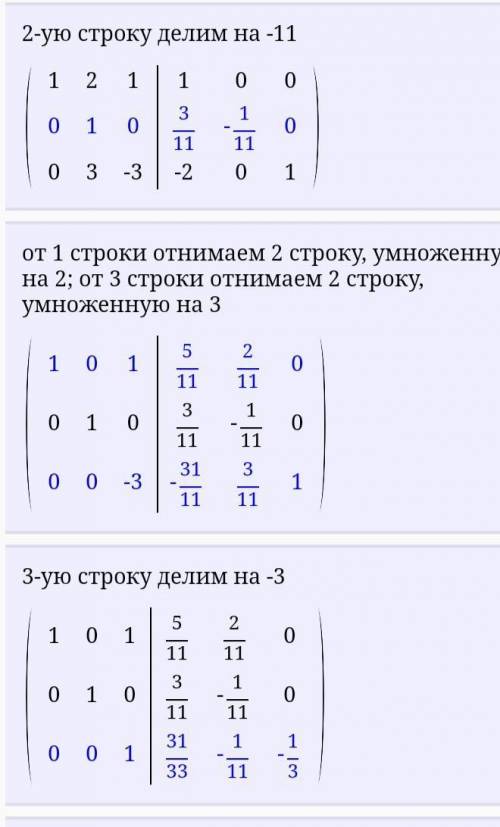
2-ую строку делим на -11
от 1 строки отнимаем 2 строку, умноженную на 2; от 3 строки отнимаем 2 строку, умноженную на 3
3-ую строку делим на -3
рис. 3:
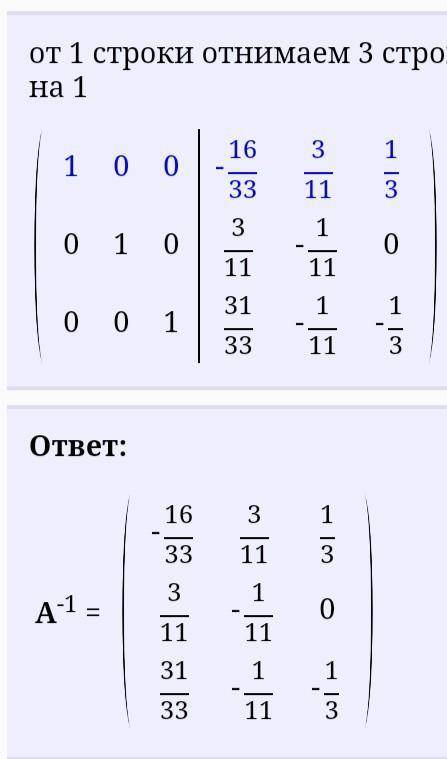
от 1 строки отнимаем 3 строку, умноженную на 1

x-20
x=20*660/100=132
660+132=792
792-100
x-10
x=10*792/100=79.2
79.2+792=871.2 тг- изначальная цена