Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
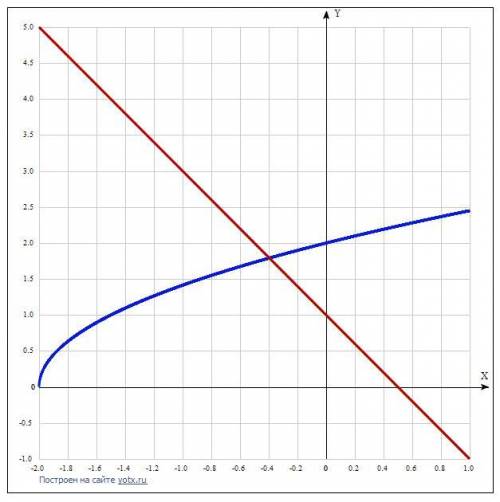
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.
В XIII−XIV веках город Кырым, или Солхат, был центром юрта (административной единицы) Золотой орды. По нему Крымом стали называть весь полуостров. Это был богатый торговый город, управляемый и частично населённый мусульманами, с большим количеством жителей-христиан — армян, греков, и итальянцев, богатевший на транзите восточных товаров из генуэзских портов — Кафы и Солдайи — на Русь, в Европу, и обратно.
В 1314 году, в начале правления хана Золотой орды Узбека, в Солхате была заложена мечеть. В 1332 году к ней добавили медресе по инициативе богатой женщины Инджибек-хатун, которая там же рядом в 1371 году была похоронена. Медресе на сегодняшний день представляет собой величественные руины, но мечеть сохранилась полностью.
Форма мечети простая, прямоугольная, крыша двухскатная. Минарет один, сбоку от входа. Портал и михраб украшены резьбой и надписями, в которых зафиксирована дата строительства. Мечеть действующая, но регулярно посещается туристами.