Обозначим количество букетов как (количество букетов), известно, что (количество букетов)>5
Обозначим количество красных цветков в одном букете, как (количество красных цветков в одном букете)
Обозначим количество белых цветков в одном букете, как (количество белых цветков в одном букете)
Обозначим количество розовых цветков в одном букете, как (количество розовых цветков в одном букете)
тогда:
(количество красных цветков в одном букете)+(количество белых цветков в одном букете)+(количество розовых цветков в одном букете) = (количество цветов в одном букете) , что нам необходимо найти
всего цветов:
(количество букетов)*(количество цветов в одном букете)
или
12+18+30=60
разложим 60 на множители
1*2*2*3*5
так как букетов больше 5 то (количество букетов) может принимать значения 6, 10, 12, 15, 20,...
с другой стороны букеты одинаковые, а значит числа
(количество красных цветков в одном букете),(количество белых цветков в одном букете),(количество розовыз цветков в одном букете)
являются делителями чисел 12, 18, и 30 соответственно
ТАКИМ ОБРАЗОМ приходим к выводу:
максимальное (количество букетов) = НОД(12;18;30)
по свойсву НОД(а*х;а*у)=а*НОД(х;у) получаем
(количество букетов)=(какой-то коэффицент)*НОД(12,18,30)=(какой-то коэффицент)*6*НОД(2,3,5)=(какой-то коэффицент)*6
получили, что (количество букетов) может принимать значения 6, 3, 2, 1
по условию (количество букетов)>5, значит составили 6 букетов
и в одном букете 60/6=10 букетов
1. Немного непонятно выражение.
2. Так как количество груш, растущих в саду, составляет 32% количества яблонь, находим:
50*0,32 = 50*32/100 = 16 груш
Найдем, какое количество вишен растет в саду (обозначим через х), если груши составляют 4/7 от количества вишен:
х*4/7 = 16
х = 16*7/4 = 28
ответ: 16 груш, 28 вишен.
3. На фото ниже.
4. Пусть первый вагон - 3х, тогда второй - х. Когда из первого вагона вышло 28 пассажиров - (3х-28), а из второго 4 пассажира (х-4), то в обоих вагонах пассажиров стало поровну. Составим уравнение:
3х - 28 = х - 4
2х = 24
х = 12 (п.) - во 2 вагоне
12*3 = 36 (п.) - в 1 вагоне
ответ: 36 пассажиров, 12 пассажиров.
5.
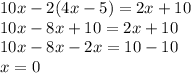
sin x = 0
x = πn, n∈Z
2) cos 2x cos 4x - sin 2x cos 4x = 1
cos (2x+4x) = 1
6x = πn
x = πn/6, n∈Z
3) Если в таком виде, как написано, то:
sinx - π/9 = 0 или cos3x + 6π/5 = 0
sinx = π/9 cos3x = -6π/5
x = (-1)^n*arcsin(π/9) + πn нет корней, т.к. 6π/5>1
А если (sin (x-π/9))(cos (3x + 6π/5))=0
sin (x-π/9) = 0 или cos (3x + 6π/5) = 0 ⇒ cos (3x + π + π/5) = 0
x-π/9 = πn - cos (3x + π/5) = 0
x = π/9 + πn 3x+π/5 = π/2 + πk
3x = π/2 - π/5 + πk
3x = 3π/10 + πk
x = π/10 + (πk)/3