Вероятности попадания из каждого орудия:
p1 = 0,6; p2 = 0,7; p3 = 0,8;
Вероятность не попасть из каждого орудия:
q1 = 1 - 0,6 = 0,4; q2 = 1 - 0,7 = 0,3 ; q3 = 1 - 0,8 = 0,2;
Только один снаряд попадет в цель:
Пусть А - событие, при котором будет только одно попадание.
А1, A2, A3 - попадание было из орудия 1,2 или 3.
A`1, A`2, A`3 - попадания не было из орудия 1,2 или 3. Это противоположные события.
Представим вероятность как сумму вероятностей несовместных событий:
P(A) = P(A1)P(A`2)P(A`3) +P(A`1)P(A2)P(A`3)+ P(A`1)P(A`2)P(A3) =
= p1 · q2· q3 + q1 · p2 · q3 + q1 · q2 · p3 =
= 0,6 · 0,3 · 0,2 + 0,4 · 0,7 · 0,2 + 0,4 · 0,3 · 0,8=1,88 ;
Только два снаряда попадут в цель:
P(A) = p1 · p2· q3 + p1 · q2 · p3 + q1 · p2 · p3 =
= 0,6 · 0,7 · 0,2 + 0,6 · 0,3 · 0,8 + 0,4 · 0,7 · 0,8 = 0.452
Хотя бы один снаряд попадет в цель:
Пусть A` - противоположное событие - ни один снаряд не попадет в цель:
P(A`) = q1 · q2 · q3 = 0,4 · 0,3 · 0,2 = 0,024
Пошаговое объяснение:
Можно предположить прямоугольник со сторонами 10 на 20 см
10 * 20 = 200 см ² будет его площадь
Ширину уменьшили на 30 %
10 * 0.3 = 3 см на столько уменьшили ширину
Длину увеличили на 80 %
20 * 0.8 = 16 см увеличили длину
Прямоугольник стал размерами
10 - 3 = 7 см ширина
20 + 16 = 36 см - длина
36 * 7 = 252 см² - будет площадь измененного прямоугольника
252 - 200 = 52 см² больше стала площадь
200 см² - 100 %
52 см² - х % х = 52 * 100 \ 200 = 26 % - на столько процентов увеличилась площадь прямоугольника
Объем начального бруска:
V₀ = abh = 30 · 50 · 90 = 135000 (см³)
Объем одной дощечки:
V₁ = a₁b₁h₁ = 5 · 40 · 60 = 12000 (см³)
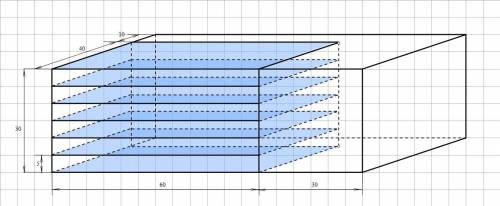
Так как ширина и высота дощечки (40 и 60 см) меньше ширины и высоты бруска (50 и 90 см), а длина дощечки (5 см) укладывается в длине бруска (30 см) 6 раз, то от бруска возможно отпилить только 6 дощечек с указанными размерами. Причем, распилы можно производить только так, как показано на рисунке.
Общий объем дощечек:
V₆ = 6 · V₁ = 6 · 12000 = 72000 (см³)
Оставшийся брусок имеет угловую форму с объемом:
V = V₀ - V₆ = 135000 - 72000 = 63000 (см³)
Несмотря на то, что оставшийся объем бруска больше объема одной дощечки, ни одной дощечки с указанными размерами из бруска выпилить больше нельзя (если только имеются в виду целые, а не составные дощечки).
Если же остальные дощечки можно делать составными (с последующим склеиванием кусочков), то оставшегося объема бруска хватит еще на 5 дощечек:
N' = V : V₁ = 63000 : 12000 = 5 (ост. 3000)
Таким образом, из указанного бруска можно получить 6 целых и 5 составных дощечек с указанными размерами, причем объем остатка от бруска составит 3000 см³.
ответ: 6 целых и 5 составных дощечек.
2)0,2*0,3*0,4 = 0,024 (2,4%)