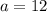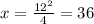Решение существует только при 
∈(-∞; 0] ∪ [12; +∞) , причем оно единственное:
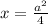
При каком наименьшем натуральном “” уравнение имеет решение?
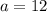
При этом имеем корень:
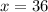
Пошаговое объяснение:
Найдем такое значение , при котором существует решение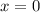 
Сначала рассмотрим случай, когда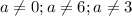 
В этом случае можно поделить обе части уравнения на ![\sqrt[]{x}](/tpl/images/1359/7534/7e667.png)
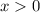
Сделаем замены:
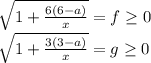
Поскольку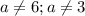 
, то данное уравнение эквивалентно системе:
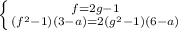
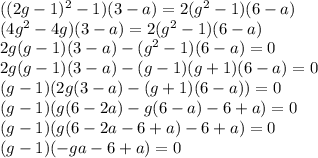
Решаем уравнение относительно замены.
Поскольку мы решаем уравнение относительно радикала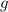 
,то корень, полученный в процессе решения, не будет обращать подкоренное выражение в отрицательное число, но тем не менее, нельзя забывать, что 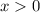, а самое главное, что 
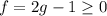, но если это неравенство выполнено, то выполнено и то, что 
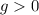. Тут надо понимать еще один не мало важный момент, что корень полученный, после решения уравнений относительно замен 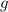и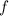 
будет одинаковым, а значит, поскольку 
, то оба из подкоренных выражений будут неотрицательны.
1) 
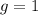
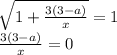
Поскольку 
тут решений нет
2)
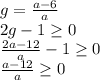
∈(-∞; 0) ∪ [12; +∞)
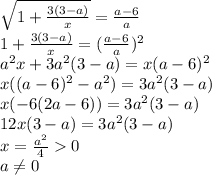
Таким образом, при ∈(-∞; 0) ∪ [12; +∞) одно решение:
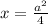
Рассмотрим теперь частные случаи:
1) 
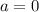
В этом случае, мы сначала обозначаем, что точно существует корень
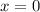
Потом, не боясь за его потерю, опять приходим к тому, что
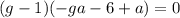
Но поскольку 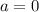, то вторая скобка превращается в константу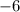 
То есть, возможно только 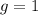, но как уже было показано выше, данное уравнение не имеет решений.
Таким образом, в этом случае, имеем одно решение.
Примечание: можно заметить, что решение 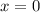точно согласуется с формулой :
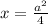, что является удобным совпадением.
То есть мы можем объединить первый и второй случай в один:
Одно решение при ∈(-∞; 0] ∪ [12; +∞)
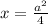
2) 
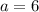
Как видим, тут решений нет
3) 
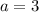
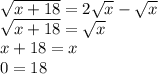
Как видим, тут решений нет.
Таким образом, наименьшее натуральное a, при котором решение существует, это:
