Пошаговое объяснение:
Раціональній дріб буде мати зміст при умові , що знаменник не дорінює 0.
Визначимо , який вирах буде мати зміст ,для цього визначимо область допустимих значень (ОДЗ)
а)
х²+9≠0
х²≠-9
оскільки будь-яке число у квадраті буде додатнім , то ОДЗ (- ∞; +∞ ),
отже вираз буде мати зміст при будь-якому значенні , що відповідає умові.
б)
х+9≠0
х≠-9
ОДЗ (-∞ ; -9) ∪(-9;+∞),
що не відповідає умові
в)
х-9≠0
х≠9
ОДЗ (-∞;9) ∪ (9 ; +∞)
не відповідає умові
г)
х²-9≠0
х²≠9
х≠±3
не відповідає умові
Вірна відповідь : а
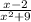
а)
Пошаговое объяснение:
Перевод: Который из выражений имеет смысл при любом значении х?
Решение. Если некоторое выражение имеет смысл при любом значении х, то область допустимых выражений совпадает с осью Ох. Последнее означает, что ОДЗ равен (-∞; +∞).
Поэтому определим ОДЗ каждого выражения:
а)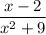 
- знаменатель x²+9≥9>0, поэтому ОДЗ: (-∞; +∞), то есть выражение имеет смысл при любом значении х;
б)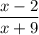 
- при x=-9 знаменатель рана 0, поэтому ОДЗ: (-∞; -9)∪(-9; +∞), то есть выражение имеет смысл не для любого значения х;
в)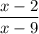 
- при x=9 знаменатель рана 0, поэтому ОДЗ: (-∞; 9)∪(9; +∞), то есть выражение имеет смысл не для любого значения х;
г)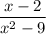 
- при x=±3 знаменатель рана 0, поэтому ОДЗ: (-∞; -3)∪(-3; 3)∪(3; +∞), то есть выражение имеет смысл не для любого значения х.
В нашем случае r = 1
Или
Если соединить все вершины правильного шестиугольника через центр, станет видно, что правильный шестиугольник состоит из 6-ти правильных треугольников, т.е. r = a