Дана функция:
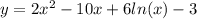
Найдем её производную:
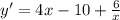
Приравняем производную к нулю:
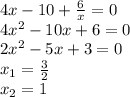
Получили 2 точки возможного экстремума. Так как 12/11 < 1.5, то точка 1.5 не попадает в данный промежуток, поэтому проверяем поведение производной в окрестностях 1.
Возьмём точку 0.95 < 1. Подставляем в производную:
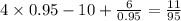
Число положительное, следовательно функция возрастает.
Берём точку 1.05 > 1. Подставляем в производную:
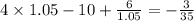
Число отрицательное, следовательно функция убывает.
Ситуация такая: слева от 1 функция возрастает, а справа – убывает, а это значит что точка 1 является наибольшим значением функции. Подставим точку 1 в функцию:
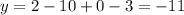
ответ: -11
ответ: 
Нужно найти вероятность того, что для открытия замка понадобится 1, 2 или 3 попытки.
Если мы найдем все эти три вероятности отдельно, а затем их сложим, то получим искомую вероятность.
Значит, вероятность того, что мы управимся за одну попытку, равна 
, по условию задачи.
Какова же вероятность, что мы сможем это сделать за две попытки? Она состоит из неудачной первой попытки (
) и удачной второй (
). Перемножаем: 
.
За три попытки считаем вероятность по аналогии: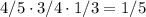 
.
Итого имеем сумму следующих вероятностей:
То есть, вероятность того, что мы откроем зАмок или замОк равна . Задача решена!
2:7=0,2857142857142857