7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть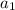 
- изначальное число и 
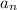- сумма цифр числа 
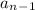. Пусть остаток при делении на 9 у числа 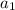- r, тогда и у числа 
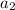остаток при делении на 9 тоже r. Но тогда и у чисел 
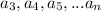остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа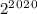 
. А он такой же, как у числа 
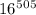, и такой же, как у числа 
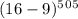, и такой же, как у числа 
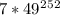, а он такой же, как у числа 
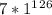, а это равно 7.
Пошаговое объяснение:
Дано:
BC=3
AB=12
CD=15
AH=HB
∠ADH=HDC
Найти:
AD - большее основание трапеции АВСD
BA - высота трапеции АВСD
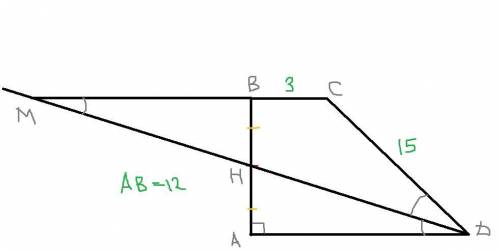
В трапеции АВСD биссектрису HD продолжим до точки M . При этом продолжим меньшее основание ВС у трапеции ABCD,также до точки M пересечения с продолжением биссектрисы HD. Исходя из сделанного дополнительного построения получаем,что углы ∠ADH=∠HDC=∠CMD . Так как ∠ADH=∠HDC=∠CMD,то треугольник MCD является равнобедренным,то есть MC=CD и поэтому сторона MC=15.
Если нам известно,что MC=15,а малое основание ВС=3,то MB=12.
Так как нам известно из условия,что AH=HB ,то опираясь на признаках равенства треугольников получаем,что ΔMBH=ΔHAD,следовательно MB=AD=12.
Высота в это случае равна AB,то есть AB=h=12
ответ: Большее основание трапеции ABCD - AD=12
Высота трапеции ABCD равна 12
2) 4(x+y) + 5(2x-y) = 4x+4y+10x-5y = 14x-y
3) 2.4(c-3b)-1.3(2c-d) = 2.4c-7.2b-2.6c-1.3d = -0.2c -7.2b-1.3d
4) -