4. Угол ABC - вписанный, следовательно он равен половине дуги, на которую он опирается. Значит, дуга ADC = 2*40 (гр.) = 80 (гр.)
Дуга ABC = 360 (гр.) - дуга ADC = 360 (гр.) - 80 (гр.) = 280 (гр.)
Угол ADC - вписанный, следовательно он равен половине дуги, на которую он опирается. Значит, угол ADC = дуга ABC/2 = 280 (гр.)/2 = 140 (гр.)
7. Угол ABC - вписанный, следовательно он равен половине дуги, на которую он опирается. Значит, дуга AC = 2*30 (гр.) = 60 (гр.)
Угол ADC - вписанный, следовательно он равен половине дуги, на которую он опирается. Значит, угол ADC = дуга AC/2 = 60 (гр.)/2 = 30 (гр.)
8. Согласно теореме Фалеса, вписанный угол, опирающийся на диаметр окружности, является прямым. Следовательно, угол ABD = 90 (гр.)
Пошаговое объяснение:
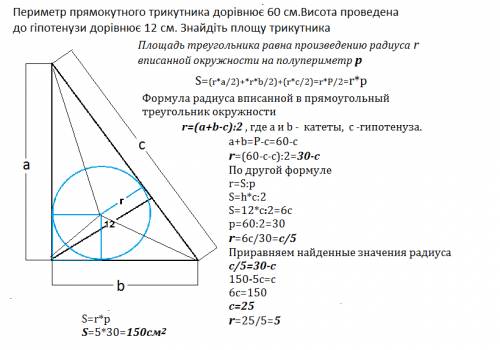
Периметр прямоугольного треугольника равен 60 см. Высота, проведенная к гипотенузе, равна 12 см. Найти площадь треугольника.
* * *
Площадь треугольника равна произведению радиуса r вписанной окружности на полупериметр р
Формула радиуса вписанной в прямоугольный треугольник окружности
r=(a+b-c):2 , где а и b - катеты, c -гипотенуза.
a+b=P-с=60-c
r=(60-c-c):2=30-c
По другой формуле
r=S:p
S=h*c:2
S=12*c:2=6c
р=60:2=30
r=6c/30=c/5
Приравняем найденные значения радиуса
c/5=30-c
150-5c=c
6c=150
c=25 см
r=25/5=5 см
S=r*p=5*30=150 см²
ответ: две бригады, работая вместе выполнят работу за 12 дней.
Пошаговое объяснение:
Принимаем задание за единицу (1). ⇒
Скорость выполнения задания первой бригадой: 1/18,
а скорость выполнения задания второй бригадой: 1/36.
Суммарная скорость выполнения задания двумя бригадами:
(1/18)+(1/36)=(2+1)/36=3/36=1/12. ⇒
Две бригады, работая вместе выполнят работу за: 1/(1/12)=12.