1. Площадь квадрата равна длине его стороны, возведённой в квадрат: 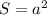 , где
, где  - это сторона квадрата. Зная площадь, можем вычислить длину стороны:
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: 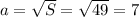 см. Периметр квадрата равен длине его стороны, умноженной на 4:
см. Периметр квадрата равен длине его стороны, умноженной на 4: 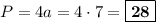 см.
см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть  см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть,
см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть, 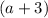 см. Составляем уравнение:
см. Составляем уравнение:
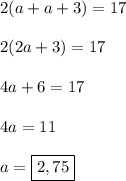
Тогда другая сторона его 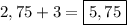 см.
см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда 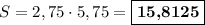 см².
см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
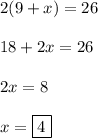
Тогда площадь прямоугольника 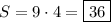 см².
см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: 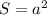 , где
, где  - это сторона квадрата. Зная площадь, можем вычислить длину стороны:
- это сторона квадрата. Зная площадь, можем вычислить длину стороны:  см. Периметр квадрата равен длине его стороны, умноженной на 4:
см. Периметр квадрата равен длине его стороны, умноженной на 4: 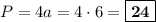 см.
см.
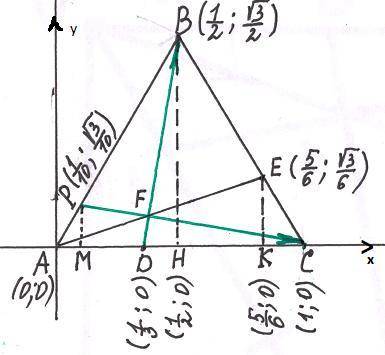
В равностороннем треугольнике ABC на сторонах AC и BC отметили точки D и E такие, что CD=2AD, BE=2CE. Обозначим точку пересечения отрезков AE и BD через F. Чему равен угол BFC?
Пошаговое объяснение:
1) Введем прямоугольную систему координат .Пусть АВ=ВС=АС=1. Пусть FC∩АВ=Р .Пусть ЕК⊥АС, ВН⊥АС, РМ⊥АС.
2) Определим координаты точек .
А(0;0) ,В(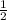 ;
;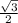 ) ,С(1;0) ,Н(0,5 ;0) ,D(
) ,С(1;0) ,Н(0,5 ;0) ,D( 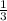 ;0) ,К(
;0) ,К( 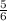 ;0) , Е(
;0) , Е(
3)Найдем координаты направляющих векторов: DB( 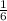 ;
;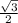 ) , РС(
) , РС( 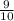 ;
;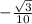 ).
).
4)Найдем скалярное произведение векторов .
DB *РС= 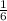 *
* 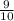 +
+ 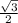 *(
*(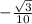 ) =
) =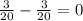 ⇒вектор DB⊥PC ⇒∠BFC=90°.
⇒вектор DB⊥PC ⇒∠BFC=90°.
=======================================
Пояснения( жуткие вычисления , слабонервным можно не читать).
1) Координаты точки Е. ΔКСЕ прямоугольный .
КЕ=СЕ*sin60= 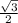 *
*  .
.
КС=СЕ*cos60= 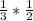 =
=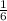 , поэтому АК= 1-
, поэтому АК= 1-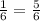 → Е(
→ Е( 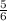 ;
;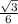 ) .
) .
2)Координаты точки В. ΔАВН- прямоугольный .
АН=НС= 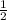 .
.
ВН=АВ*sin60=1* 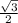 =
=
3)Ищем координаты точки Р
а)ΔВDC , по т. Менелая 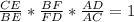 ,
, 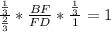 ,
, 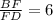 .
.
б)ΔАВD , по т. Менелая 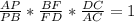 ,
, 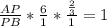 ,
, 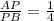 ,
,
AP= =
= 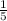 .
.
в)ΔАРМ прямоугольный .
РМ=АР*sin60=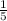 *
* 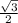 =
= 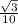 .
.
АМ=АР*cos60= 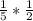 =
=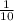 → P (
→ P ( 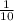 ;
;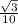 ) .
) .