Вычеслите объем параллепипеда, если длина 5 см, ширина 10см, и высота 15 дм.

👇

Увидеть ответ

Ответ:

buniatyansona

20.02.2020

15 дм=150 см
V=5*10*150=7500см^3=7,5дм^3

4,5(61 оценок)

Открыть все ответы

Ответ:

Ekateika

20.02.2020

При умножении десятичный дробей количество цифр после запятой равно сумме количества цифр после запятой первого и второго числа (отбрасывая нули в конце, если они появятся).

Часть первая.

Первый пример:

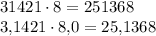
$31421 \cdot 8=251368\\3{,}1421 \cdot 8{,}0=25{,}1368$

После 3,1421 четыре цифры после запятой, после 8 ни одной цифры после запятой (0 не считается — он для наглядности), поэтому после запятой в произведении будут 4+0=4 цифры.

По аналогии

Второй пример:

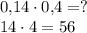
$0{,}14 \cdot 0{,}4=?\\14 \cdot 4=56$

Чтобы правильно поставить запятую, поставим перед числом 56 несколько нулей (по определению десятичной записи они не изменят числа):

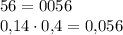
$56=0056\\0{,}14 \cdot 0{,}4=0{,}056$

Третий пример:

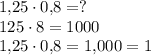
$1{,}25 \cdot 0{,}8=?\\125 \cdot 8=1000\\1{,}25 \cdot 0{,}8=1{,}000=1$

Четвёртый пример:

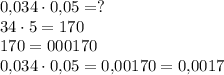
$0{,}034 \cdot 0{,}05=?\\34 \cdot 5=170\\170=000170\\0{,}034 \cdot 0{,}05=0{,}00170=0{,}0017$

Часть вторая. Примеры для закрепления

Первый

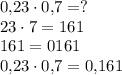
$0{,}23 \cdot 0{,}7=?\\23 \cdot 7=161\\161=0161\\0{,}23 \cdot 0{,}7=0{,}161\\$

Второй

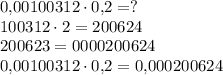
$0{,}00100312 \cdot 0{,}2=?\\100312 \cdot 2=200624\\200623=0000200624\\0{,}00100312 \cdot 0{,}2=0{,}000200624$

Третий

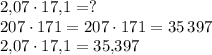
$2{,}07 \cdot 17{,}1=?\\207 \cdot 171=207 \cdot 171=35\,397\\2{,}07 \cdot 17{,}1=35{,}397$

Чётвёртый

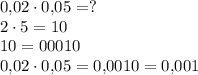
$0{,}02 \cdot 0{,}05=?\\2 \cdot 5=10\\10=00010\\0{,}02 \cdot 0{,}05=0{,}0010=0{,}001$

Пятый

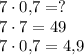
$7 \cdot 0{,}7=?\\7 \cdot 7=49\\7 \cdot 0{,}7=4{,}9$

4,4(4 оценок)

Ответ:

idzzzid666

20.02.2020

чтобы найти площадь диагонального сечения надо сначала найти диагональ, её можно найти по теореме пифагора. диагональ будет равна 5√2, следовательно площадь диагонального сечения будет равна 25√2 см2

а объем куба будет равен 5*5*5= 125 см3

Пошаговое объяснение:

Для геометрических тел с правильным многоугольником в основании можно провести диагональ последнего. Если эту линию спроецировать к вершине (для пирамиды) либо вершинам, например, для куба или параллелограмма, получим диагональное сечение объёмного тела. Если площадь куба вычисляется путём возведения длины стороны в квадрат, то с размером занимаемой сечением поверхности дело сложнее.

Секущая площадь куба имеет форму прямоугольника, где одна пара сторон представлена рёбрами кубика, вторая – диагоналями граней. Для вычисления её площади нужна только длина ребра правильного прямоугольника, ведь одна из них выполняет роль высоты. Длина диагонали для треугольников, где высота – это гипотенуза, а рёбра – катеты, определяется по формуле a*√2. Занимаемая диагональным сечением куба площадь равняется:

S = a * a * √2 = a²*√2.

Диагональное сечение куба - это прямоугольник, у него меньшая сторона совпадает с ребром, а большая - с диагональю грани (основания). Таким образом, чтобы найти площадь диагонального сечения куба, нужно воспользоваться формулой площади прямоугольника: S(пр) = a * b.

4,4(19 оценок)

Это интересно:

Кулинария-и-гостеприимство

24.10.2021

Как законсервировать томатный соус...

Семейная-жизнь

02.02.2020

Как показать почтение умершему знакомому...

Компьютеры-и-электроника

01.08.2020

Как закрывать приложения на iPhone, iPad и iPod Touch: инструкция для начинающих...

Компьютеры-и-электроника