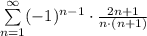
Исследуем этот ряд на абсолютную сходимость.
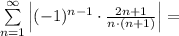
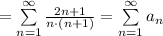
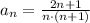
Рассмотрим ряд
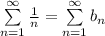
Используем предельный признак сравнения:
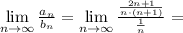
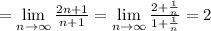
Значит ряды 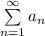 и
и 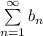
сходятся или расходятся одновременно, но ряд
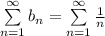
это гармонический ряд, который расходится. Значит и ряд
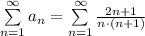
расходится.
Исследуем данный в задании ряд на условную сходимость. Используем признак Лейбница. Ряд знакочередующийся.
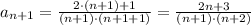
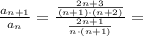
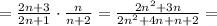
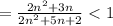
т.к. 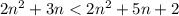 ⇔
⇔ 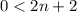 ⇔
⇔ 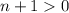 .
.
То есть 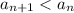 .
.
То есть последовательность 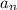 монотонно убвывает.
монотонно убвывает.
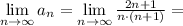
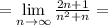
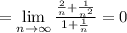
То есть последовательность 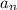 монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
монотонно убвывает и стремится к нулю. Итак, по признаку Лейбница, исходный ряд сходится.
ответ. Сходится условно.
Пошаговое объяснение: видим два прямоуг. подобных треугольника, их стороны пропорциональны
3:1=1,8 : х 3х = 1,8 х = 0,6(м)