тааак ну смотри сторона первого квадрата 2 см так как у него 4 стороны: периметр 8 делим на 4 = 2, периметр второго квадрата это 8 * 3 тоесть 24 а если 24 : 4 то будет 6. отвечаем на первый вопрос ВО сколько раз сторона первого квадрата меньше второго 6 : 2 = 3 в 3 раза. на второй вопрос про площадь что бы найти площадь нужно длинну умножить на ширину тут и длинна и ширина равна площадь первого квадрата 2 * 2 = 4 площадь второго 6 * 6 = 36 36 делим на 4 равно 9.
пишем так:
1)8:4=2(см)-сторона первого квадрата.
2)8*3=24(см)-периметр второго квадрата.
3)6:2=3(раза)
4)2*2=4(см в квадрате) (над см пиши маленькую двоечку)-площадь 1-ого квадрата
5)6*6=36(см в квадрате)-площадь 2-ого квадрата
6)36:4=9(раз)
ответ:сторона первого квадрата в 3 раза меньше второго, площадь второго квадрата в 9 раз бальше площади первого
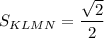
Пошаговое объяснение:
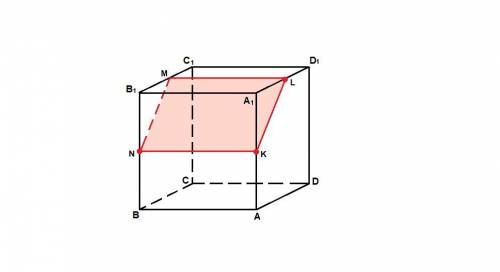
К - середина АА₁,
N - середина ВВ₁,
L - середина A₁D₁.
Соединяем точки N и К, K и L, так как каждая пара лежит в одной грани.
_______________
Отрезок, соединяющий середины противоположных сторон квадрата, параллелен другой паре сторон квадрата и равен стороне квадрата:
В₁N║A₁K так как лежат на противоположных сторонах квадрата,
В₁N = A₁K как половины равных отрезков, ∠NВ₁А₁ = 90°, значит NВ₁А₁K - прямоугольник, ⇒ NK║A₁B₁, NK = A₁B₁.
________________________
KN║A₁B₁ как отрезок, соединяющий середины противоположных сторон квадрата, значит, А₁В₁║(KLN).
Пусть М - середина В₁С₁. Тогда LM║A₁B₁.
Соединяем точки M и N.
KLMN - искомое сечение.
KN║A₁B₁, KN = A₁B₁,
LM║A₁B₁, LM = A₁B₁, значит KLMN - параллелограмм.
A₁L - проекция KL на плоскость (А₁В₁С₁), A₁L⊥A₁B₁, ⇒KL⊥A₁B₁ по теореме о трех перпендикулярах, ⇒
KL ⊥ KN, значит KLMN - прямоугольник.
KN = A₁B₁ = 1, так как куб единичный.
ΔKA₁L: ∠KA₁L = 90°, по теореме Пифагора
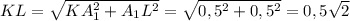
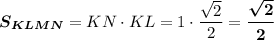
б)-|6|
в)-(-2.8)
г)3.4/2
д)-(-3/11)