Множество A ∩ B состоит из двух точек (0, -2) и (2, 0); A ∩ B = {(0, -2), (2, 0)}
Пошаговое объяснение:
Пересечение двух множеств A и B (обозначается A ∩ B) образуют элементы, которые входят в A и в B одновременно.
Поскольку в первое множество входят все пары чисел (x, y), удовлетворяющие условию x² + y² = 4, а во второе — условию x - y = 2, то A ∩ B — все пары (x, y), удовлетворяющие системе из двух уравнений
Остаётся решить эту систему уравнений. Это можно сделать графически или аналитически.
Аналитическое решениеВозведём второе уравнение в квадрат (получится x² - 2xy + y² = 4) и вычтем полученное из первого уравнения.
Тогда 2xy = 0, откуда x = 0 или y = 0.
Если x = 0, то, поскольку x - y = 2, y = x - 2 = 0 - 2 = -2; (0, -2) — первая точка, входящая в пересечение.
Если y = 0, то x = y + 2 = 2; (2; 0) — вторая точка.
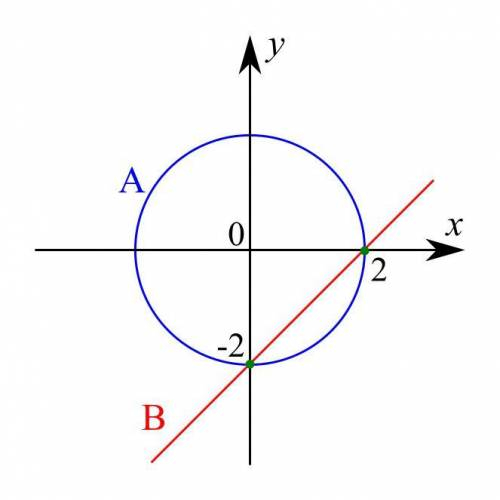
Графическое решениеПервое уравнение системы (его удобно переписать в виде x² + y² = 2²) задаёт на плоскости Oxy окружность с центром в начале координат и радиусом 2.
Второе уравнение задаёт прямую, для построения которой достаточно знать две точки. Подойдут, например, (0, -2) и (2, 0).
Пересечение множеств, которые заданы линиями на плоскости, — просто пересечение этих линий.
Окружность и прямая пересекаются в двух точках (0, -2) и (2, 0). Эти точки и составляют искомое пересечение.
Відповідь:
4. 1
5. 396
6. 12
Покрокове пояснення:
Завдання 4
НСД (35 ; 18)
35 | 5 18 | 3
7 | 7 6 | 3
1 | 2 | 2
1 |
Для НСД беремо спільні пари чисел.
Оскільки тут ні один простий дільник не збігається, то числа взаємно прості, тобто:
НСД (35 ; 18) = 1
Завдання 5
НСД (792 ; 1188)
792 | 2 1188 | 2
396 | 2 594 | 2
198 | 2 297 | 3
99 | 3 99 | 3
33 | 3 33 | 3
11 | 11 11 | 11
1 | 1 |
Для НСД беремо спільні пари чисел.
Тут такі будуть: 2, 2, 3, 3, 11
НСД (792 ; 1188) = 2·2·3·3·11 = 396
Завдання 6
Щоб скласти однакові комплекти, в яких порівну книжок, потрібно, щоб кожна кількість книжок націло ділилася на кількість комплектів!
Тобто нам потрібен найбільший спільний дільник для 3 чисел (Найбільший, тому що питання, яку найбільшу кількість комплектів можна скласти).
НСД ( 24 ; 36 ; 48 )
24 | 2 36 | 2 48 | 2
12 | 2 18 | 2 24 | 2
6 | 2 9 | 3 12 | 2
3 | 3 3 | 3 6 | 2
1 | 1 | 3 | 3
1 |
Для НСД беремо спільні пари чисел.
Тут такі будуть: 2, 2, 3
НСД ( 24 ; 36 ; 48 ) = 2·2·3 = 12