Пусть не так, и Р и Q - многочлены степени не ниже 1.
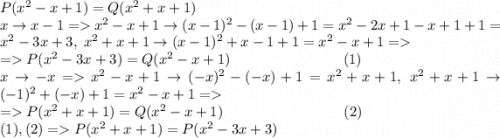
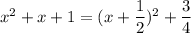- парабола с вершиной в точке 
, ветви направлены вверх.
- парабола с вершиной в точке 
, ветви направлены вверх.
Пусть подобными действиями было получено значение 
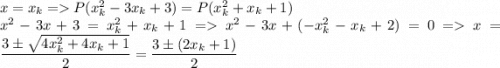
Выберем 
. Получим, что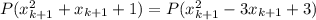 
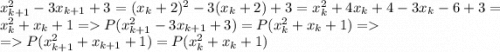
Т.е. построена монотонно возрастающая последовательность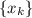 
такая, что 
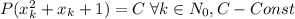. Очевидно, т.к. последовательность не ограничена сверху, то в ней бесконечное число членов => многочлен 
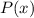принимает значение 
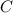в бесконечном числе точек => тогда он будет иметь вид 
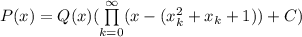, а значит его степень бесконечна, что невозможно.
А тогда 
, откуда 
, следовательно 
. Т.е. на множестве 
с бесконечным числом элементов многочлен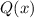 
принимает значение 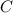. А тогда, по аналогии с предыдущим пунктом, 
Ч.т.д.
всего 7000 из этого 700 трава, 700 кора, и 4200 веток
7000-700-700-4200= 1400