Общая схема для построения графиков функций
1. Найти область определения функции D(y): x ∈ (-∞; +∞).
2. Найти точки пересечения графика функций с осями координат.
- с осью Оу при х = 0. Получаем у = 0 (точка О(0; 0)).
- с осью Ох при у = 0.
Надо приравнять:
-x^4+8x = 0,3. Исследовать функцию на четность или нечетность.
Проверим функци чётна или нечётна с соотношений:
f = f(-x) и f = -f(-x).
Итак, проверяем:
- x^{4} + 8 x ≠ - x^{4} - 8 x.
- x^{4} + 8 x ≠ - -1 x^{4} - - 8 x.
- Нет, значит, функция не является ни чётной ни нечётной
4. Исследовать функцию на периодичность - не периодична.
5. Найти промежутки монотонности и точки экстремума функции.
Для того, чтобы найти экстремумы, нужно решить уравнение
\frac{d}{d x} f{\left (x \right )} = 0 (производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
y' = - 4 x^{3} + 8 = 0.
Корни этого ур-ния
x_{1} = \sqrt[3]{2}
Значит, экстремум (он один) в точке: (∛2; 6∛2).
Это максимум, так как производная переходит от плюса к минусу
Интервалы возрастания и убывания функции:
Где производная положительна - функция возрастает, где отрицательна - там убывает.6. Найти промежутки выпуклости и точки перегиба функции.
Вторая производная равна -12х².
Где вторая производная меньше нуля, там график функции выпуклый, а где больше - вогнутый.
Поэтому график только выпуклый.
7. Найти асимптоты функции - их нет.
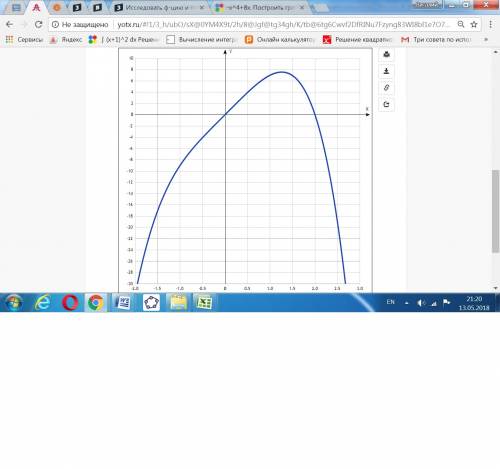
8. По результатам исследования построить график - дан в приложении .
2х1-х2/3=24
2*3х2/2- х2/3=24
18х2/6-2х2/6=24
16х2=144
х2=9
х1=13,5