7. 
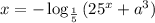
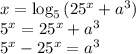
Пусть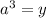 
, количество корней от этого не изменится.
Рассмотрим функцию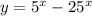 
:
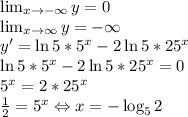
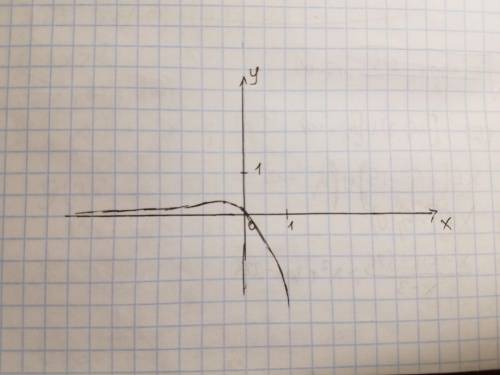
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно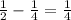 
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
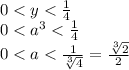
ответ: ![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
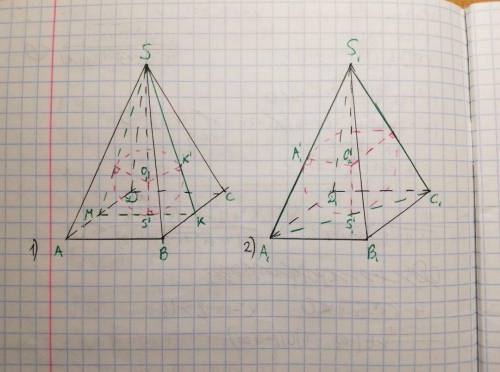
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
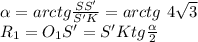
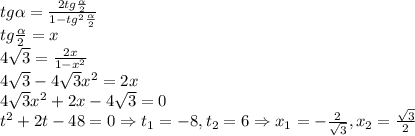
Учитывая, что угол находится в первой четверти,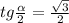 
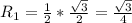
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
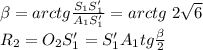
Решая аналогичное уравнение, получаем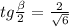 
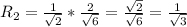
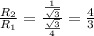
ответ: 4 : 3
ответ:
3. з цифр «4», «7», «9» числа. скільки можна скласти: а) трицифрових чисел так, щоб жодна з них не повторювалась; б) трицифрових чисел; в) двоцифрових чисел так, щоб жодна з них не повторювалась; г) двоцифрових чисел?
а)
б)
в)
г)
7. скільки різних дільників має число 2310?
розкладемо число 2310 на прості множники і складатимемо їх різні добутки (від 1 до 5 множників), тобто скла- датимемо різні підмножини. 2310 = 2 *3⋅5* 7⋅11 — усього п’ять множників. тоді маємо:
6. яку кількість різних натуральних чисел можна скласти з цифр 0, 2, 3, 4, щоб в кожне таке число кожна цифра входила не більше одного разу?
одноцифрових =
двоцифрових =
трицифрових =
чотирицифрових =
всього = 3+9+18+18 = 48
10. у ящику 20 деталей, серед яких 4 браковані. скількома способами можна взяти: а) 5 деталей; б) дві браковані; в) одну браковану і чотири стандартні; г) шість деталей, серед яких хоча б одна бракована; д) дві однакові за якістю?
а)
б)
в)
21. знайти ймовірність того, що дні народження 12 осіб припадуть на різні місяці року.
n = 1212
m = 12!
p(a) =
22. студент прийшов на екзамен підготувавши 20 з 25 питань, екзаменатор задав йому 3 питання. знайти ймовірність тго, що студент знає відповіді на всі питання.
аі – випадкова подія
р(а) =
= 0,497
27. на книжковій полиці випадковим чином розставляють 4 книги з економіки і три книги з ії. яка ймовірність того, що книги з одного предмета стоятимуть поруч?
p4*p3 =
30. десять осіб випадковим чином сі за круглий стіл. знайти ймовірність того, що чотири певні особи опиняться поруч.
р(а) = загальна кількість рівноможливих способів розмістити 10 осіб на 10 місцях за круглим столом дорівнює кількості перестановок із 10 елементів, тому n! = 10!
4 певні людини можна розмістити поруч 4! способами. інших 6 людей можна розмістити 6! способами. за круглим столом (10 місць) пару певних 4 людей можна розмістити 10 спосо- бами.
m = 4! *6! *10
p(a) =
32. а та в і ще 8 осіб стоять у черзі. знайти ймовірність того, що між а та в стоять три особи.
n = 2+8 = 10 r =3
p(a) =
33. з урни, в якій лежать 12 білих і 8 червоних кульок, беруть послідовно дві кульки. відомо, що перша кулька виявилась білою. яка ймовірність того, що друга кулька виявиться: а) білою; б) червоною?
а – взята біла кулька
в – взята червона кулька
якщо першою взяли білу кулю, то в урні залишилося 11 білих кулі та 8 червоних, тому
а)
пошаговое объяснение:
