Дано:
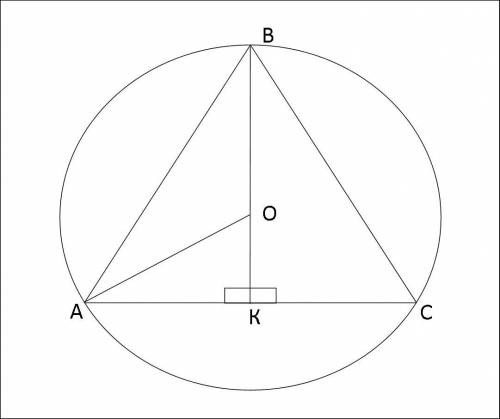
(O;R) - описанная окружность
C=50π
АВ=ВС
ВК⊥АС
ВК=32см
Найти Р (периметр)
Решение.
1) C=50π
C=2πR
2πR=50π
R=25 см
AO=OB=R=25 см
2) BK ⊥ AC => ∠AKB=90°
3) BK=32 см
OK=BK-OB
OK=32 - 25 = 7см
3) Рассмотрим ΔAOB, в нем =>
AO=25 см
OK=7 см
∠AKO=90°
По теореме Пифагора
AK² = AO² - OK²
AK²=625-49 = 576
AK=√576 = 24 см
4) AC = 2AK= 48 см
5) В ΔABK => ∠АКВ=90°
По теореме Пифагора
AB² = AK² + BK²
AB² =576+1024 =1600
AB = √1600 = 40 см
AB=BC=40 см
6) 40+40+48=128 см - периметр ΔАВС.
Вiдповiдь: 128 см
ответ:
пошаговое объяснение:
при умножении степеней с одинаковым основанием показатели складываются, а при делении отнимаются, ну и основание остаётся неизменным
с⁷+с³=с⁷⁺³=с¹¹ х⁸: х⁴=х⁸⁻⁴=х⁴
а³ а
х⁶ с⁵
и так далее, плохо видно
4x-2x-14=16-2x
2x-14=6-2x
-2x-2x=6+14
4x=20
X=5