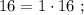
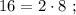
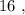т.е.: 
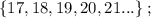
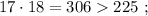
каждое – будет, очевидно, больше чем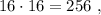 
т.е. больше 
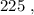а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.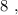
т.е.: 
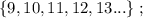
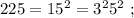
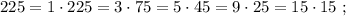
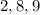и 
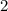и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы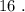 
и никаких натуральных чисел нет. и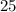 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы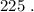 
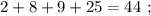
пусть сторона в 12 см будет основанием (обозначим ее a).
проекция второй стороны (обозначим ее b) на основание имеет длину 5 * 3/5 = 3 см.
По теореме Пифагора высота треугольника h = sqrt(25-9) = 4 см.
Площадь треугольника = S = ah/2 = 12*4/2 = 24 кв.см.
Обозначим третью сторону c. Ее проекция на основание имеет длину = 12 - 3 = 9
И по Пифагору ее длина = sqrt(16+81) = sqrt(97)
Очевидно, что строна a=12 см самая большая в треугольнике, а значит максимальным будет угол ей противолежащий (т.е. угол между сторонами b и c)
Площадь треугольника равен произведению длин сторон треугольника на половину синуса угла между ними, значит синус максимального угла равен
sin A = S*2/(c*b) = 24*2/5/sqrt(97) = 9.6 / sqrt(97)
ответ
а) sqrt(97)
б) 24
в) 9.6 / sqrt(97)
94*64=6016
45*36=1620
33*72=2376
105*67=7035
507*18=9126
63*704=44352
71*903=64113
230*17=3910
420*31=13020
32*240=7680
57*130=7410
461*84=38724
318*49=15582
65*174=11310
92*536=49312