Каждую из этих фраз он мог сказать про мальчика или про девочку.
1. Если первую фразу он сказал применительно к мальчику, то у него было 4 сына: этот самый мальчик и его три брата.
1.1. Если вторую фразу он сказал тоже про мальчика, то у этого мальчика сестер, как и братьев по 3. Итого: 3+3+1=7 детей
1.2. Если вторую фразу он сказал про девочку, то у нее братьев будет 4, а значит и сестер тоже 4. Итого: 4+4+1=9 детей
2. Если первую фразу он сказал применительно к девочке, то у него было только 3 сына.
2.1. Если вторую фразу он сказал про мальчика, то у этого мальчика будет только 2 брата, соответственно сестер столько же. Итого: 2+2+1=5 детей
2.2. Если вторую фразу он сказал про девочку, то у нее 3 брата и соответственно 3 сестры. Итого: 3+3+1=7 детей
Максимальное количество детей - 9
ответ: 9
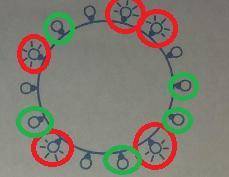
Чтобы среди любых трех подряд идущих лампочек хотя бы две горели, каждую негорящую лампочку должны с друх сторон окружать по две горящие. Таким образом, в результате все лампочек можно будет разделить на группы, состоящие из одной негорящей и двух горящих лампочек. Другими словами одной негорящей лампочке должно соответствовать две горящие.
Так как всего лампочек 14, то только 4 группы будут полными, то есть содержать негорящую лампочку. В последней группе будут строго две горящих лампочки.
Итак, 4 лампочки могут остаться негорящими. Значит заменить нужно 5. Пример такой замены на картинке.
ответ: Б) 5
9×/11 = 6у/7
извторого уравнения: х =11у/21
подставим это значение для х в первое уравнение:
у =11у/21 =172
31у/21 = 172 откуда у = 903/8 =112 и 7 в остатке