В этой задаче, зная синус угла Т, надо определить его тангенс.
tg T = sin T/√(1 - sin² T) = (√29/7)/(√(1 - (29/49)) = √(29/20).
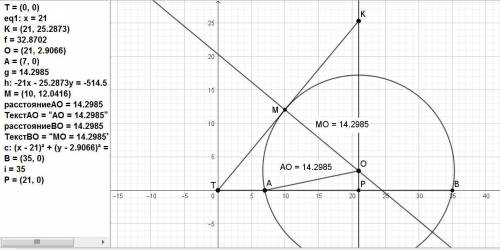
Центр О окружности находится на прямой х = (7 + 35)/2 = 21.
Примем расстояние точки О от стороны TF, равным у.
Длина отрезка РК (как катета) равна 21*tg T = 21*√(29/20).
Точка М - точка касания окружности с прямой ТЕ, ОМ - радиус R.
Угол МОК равен углу Т как взаимно перпендикулярный.
Отрезок ОК = R/cos T = R/(√(1 - (29/49)) = 7R/√20.
Составим уравнение: РО + ОК = РК. Подставим данные.
у + (7R/√20 = 21*√(29/20),
у*√20 + 7R = 21*√29.
Теперь рассмотрим треугольник ОАР.
R² = (21 - 7)² + y².
Решаем систему с двумя неизвестными R и у.
{y*√20 + 7R = 21*√29.
{R² = (21 - 7)² + y².
Решение системы: R = 77/√29 ≈ 14,2985.
y = 7*√(5/29) ≈ 2,90659.
6
Пошаговое объяснение:
При любом натуральном x числа x+2, x+3 и x+4 - это три последовательных числа, хотя бы одно из них обязательно делится на 2, и еще хотя бы одно (может быть то же самое) делится на 3.
Поэтому произведение x(x+2)(x+3)(x+4) обязательно делится на 6.
Если a = n/y - наименьшее, то знаменатель y - наибольший.
Так как произведение n/y*x(x+2)(x+3)(x+4) должно быть натуральным при любом натуральном x, то y должен быть с одной стороны наибольшим, а с другой стороны, он должен быть делителем x(x+2)(x+3)(x+4).
y = 6.
a = 1/6.