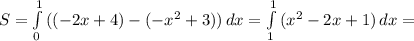
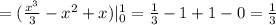 ед²
ед²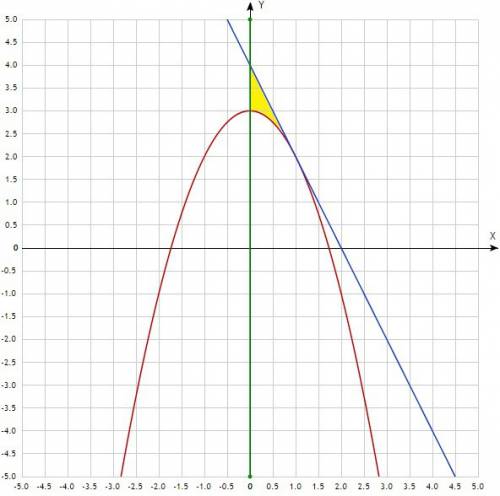
Y = x² - парабола (на рисунке синяя линия)
х = 3 - прямая перпендикулярная оси абсцисс, проходящая через точку (3,0) (зелёная линия на рисунке)
y = 0 - прямая, совпадающая с осью абсцисс (красная линия на рисунке)
Найдём ещё одну прямую, которая ограничивает параболу по иксу. Для этого в уравнение параболы подставляем y=0 и решаем уравнение относительно икса: x = 0 - ещё одна прямая перпендикулярная оси абсцисс (левая зелёная линия).
В итоге получается область серого цвета, площадь которой надо найти. Площадь находится с определённого интеграла от параболы в пределах от х=0 до х=3 (это будут пределы интегрирования).
Пошаговое объяснение:
Жизнь — это череда вопросов, на которые каждому из нас приходится искать ответы. Мы сталкиваемся с ними каждый день. Нам задают их наши друзья, незнакомые нам люди или мы ставим их перед собой сами.
Кто ты? Вопрос, на который можно дать самый разный ответ. Кто ты по национальности? Кто ты по профессии? Кто ты по религиозным убеждениям? ответы на эти вопросы для кого-то могут быть сложными, для кого-то наоборот быть очевидными, кого-то поставят в тупик. ответы могут меняться со временем, могут появляться, если человек сделал выбор, который раньше был для него слишком сложным. Человек может смело заявить о том кто он, или скрывать это от окружающих. ответ на любой вопрос — это маленький выбор.
Вопросы, от которых не уйти
Но самые важные вопросы — это те, которые мы задаем себе. Мы можем не отвечать на них, можем отвечать чесно или пытаться сорвать, можем рассказывать о них близким или скрывать это глубоко внутри себя. Но после того, как мы задали себе тот или иной вопрос, мы всегда пытаемся найти ответ на него, даже если сами этого не замечаем.
Кто я? Рано или поздно этот вопрос возникает перед каждым. И могут уйти дни, месяцы и даже годы на поиски ответа.
Я задавала себе этот вопрос много раз. Пытаясь ответить, сталкивалась с десятками новых вопросов, которые заставляли смотреть на себя с другой стороны. Кто я? Прежде всего я человек. Я часть этого огромного, сложного мира. Я могу быть юристом или врачом, смелой или напуганной, спортсменкой или ученой, но я всегда остаюсь человеком. Человеком, которому не все равно на судьбы других. Человеком, который хочет принимать правильные решения, но не всегда справляется с поставленной задачей. Человеком, который тем, кто нуждается в нём. Я хочу всегда оставаться честной, в первую очередь, перед самой собой. Я хочу дарить людям тепло, и стараться не делать им больно. Мне кажется, что каждый из нас должен быть причиной чужого счастья. И когда-нибудь, я хочу смело сказать, что я человек, который делал мир вокруг немного лучше, а людей более счастливыми.
Если каждый из нас сумеет сделать счастливым другого человека, хотя бы одного, на земле все будут счастливы.