Пошаговое объяснение:
1. 1) 30 + 0,1*30 = 30 + 3 = 33 (руб) - стоимость билета после повышения цены.
2) 100 / 33 =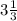 
(поезд.) - поездок.
ответ: На 3 поездки.
2 1) 8*10 = 80 (м^2) - площадь пола.
2) 80*0,4 = 32 (кг) - нужно для покраски.
32 кг краски можно получить из семи банок по 5кг.
ответ: 7.
3 Если точка принадлежит графику функции, то её координаты удовлетворяют уравнению.
А (1;2): 2 = 3*1 - 1
2 = 2 - верно, следовательно A(1;2) принадлежит графику.
B (0;-1): -1 = 3*0 - 1
-1 = -1 - верно, следовательно B(0;-1) принадлежит графику.
С (3;8): 8 = 3*3 - 1
8 = 8 - верно, следовательно C(3;8) принадлежит графику.
Д (2;4): 4 = 3*2 - 1
4 = 5 - неверно, следовательно Д(2;4) не принадлежит графику.
ответ: A,B,C.
4 
Одним з відомих нам прикладів такого розкладання є розподільна властивість множення a(b + с) = ab + ас, якщо її записати у зворотному порядку: аb + ас – a(b + с). Це означає, що многочлен аb + ас розклали на два множники а і b + с.
Під час розкладання на множники многочленів із цілими коефіцієнтами множник, який виносять за дужки, обирають так, щоб члени многочлена, який залишиться в дужках, не мали спільного буквеного множника, а модулі їх коефіцієнтів не мали спільних дільників.
Розглянемо кілька прикладів.
Приклад 1. Розкласти вираз на множники:
1) 8m + 4;
2) at + 7ар;
3) 15а3b – 10а2b2.
Р о з в’ я з а н н я.
1)
Спільним множником є число 4, тому
8m + 4 = 4 . 2m + 4 ∙ 1 = 4(2m + 1).
2) Спільним множником є змінна а, тому
At + 7ap = a(t + 7p).
3) У даному випадку спільним числовим множником є найбільший спільний дільник чисел 10 і 15 – число 5, а спільним буквеним множником є одночлен а2b. Отже,
15а3b – 10а2b2 = 5а2b ∙ 3а – 5a2b ∙ b = 5а2b(3а – 2b).
Приклад 2. Розкласти па множники:
1) 2m(b – с) + 3р(b – с);
2) х(у – t) + c(t – у).
Р о з в ‘ я з а н н я.
1) У даному випадку спільним множником є двочлен b = c.
Отже, 2m(B – С) + 3р(B – C) = (b – с)(2m + 3р).
2) Доданки мають множники у – t і t – у, які є протилежними виразами. Тому в другому доданку винесемо за дужки множник -1, одержимо: c(t – у) = – с(у – t).
Отже, х(у – t) + c(t – у) = х(у – t) – с(у – t) = (у – t) (х – с).
? -- 6,65 т
1) 6,65 : 4,75 = 1,4 раза больше вторая плита бетона
2) 2,5*1,4=3,5 куб м - объём второй плиты